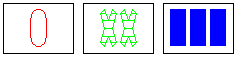
 The game is played by finding sets of three cards that are all the
same, or all different, across four independent "facets" or
"dimensions". These dimensions are: number, shape, color, and fill.
Each of these dimensions has three possible values. Number has: one,
two, or three; color has: red, green, or blue; shape has: rectangle, X,
or O; and fill has: open, striped, or solid.
The game is played by finding sets of three cards that are all the
same, or all different, across four independent "facets" or
"dimensions". These dimensions are: number, shape, color, and fill.
Each of these dimensions has three possible values. Number has: one,
two, or three; color has: red, green, or blue; shape has: rectangle, X,
or O; and fill has: open, striped, or solid.Here are three cards that demonstrate all twelve values:

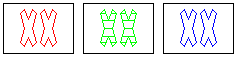
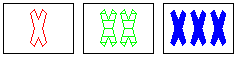
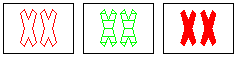

At their Web site, the people who invented SET? suggest it is an excellent vehicle for exercising both halfs of your brain. Because the game involves objective rules, players must exercise "left brain" logical, sequential problem solving. However, to find the sets, players must examine the two dimensional arrangement of cards and locate patterns with "right brain" intuitive, spatial perception.
"To effectively employ creative thinking requires use of both left and right sides of your brain. Both right brain thinking skills, and whole brain thinking receive little attention in school. They remain underdeveloped as we go through life because only a few occupations such as a football quarterback, pilot, or artist require them. However, everyone will gain by developing them. Every time you find a set you are using your whole brain and increasing your potential to be creative."
The total number of cards in a SET deck is 81. This is the number of permutations of three variables that each take on three possible values [(3 numbers) * (3 colors) * (3 shapes) * (3 fills) = 81].
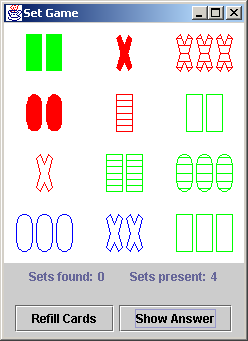
Twelve cards are initially displayed on the table. As players identify and pick up sets, the holes are filled by dealing replacement cards. The game is over when all the cards have been dealt, and no more sets can be formed. The maximum number of sets is 27. Because each individual card can participate in quite a few set, it is possible to find yourself at the end of the game with several cards that cannot be matched.
Only with conscious effort, do we aspire to, and mature in practicing, the art of abstraction. Grady Booch has suggested, "Only about 20-30% of software developers are probably really good at OO abstraction. That doesn't mean the remaining 70-80% are inadequate. Rather, this is a recognition of the fact that some people are better than others at looking at the world and discovering or inventing abstractions of reality."
The practice of abstraction can be strongly linked to the pattern recognition and spatial perception of right-brain thinking skills. The practice of programming (tied as it has been to sequence, selection, and iteration) is routinely prejudiced towards the logical orientation and linear perception of left-brain thinking skills. To succeed in our domains of ever expanding complexity, software architects and practitioners must integrate and leverage their "whole" brain.
Years ago, I heard a definition for innovation - the ability to see what everyone else has seen and think what no one else has thought. So much of this art referred to as "seeing" is really the ability to discern patterns that have heretofore gone unharvested. The SET game is an excellent vehicle for bolstering one's powers of discovery. Software design is a prime beneficiary of expanded powers of discernment.
To the degree that the act of software design remains a discipline characterized by creativity and craftsmanship, there is no substitute for multi-disciplinary powers of perception. Whether these additional dimensions of insight come from mathematical card games, or the competing world views of software design paradigms; every tool we can bring to bear on the systems we build will result in a whole that is greater than the sum of its parts.
Learn and leverage as many paradigms as possible.
The nine iterations are:
Iteration 4 is a remarkable puzzle where insight and data structure will make all the difference. Once weve laid the foundation with an interesting representation, iteration 5 is easy.
How can the validity of a set be evaluated? Iteration 8 is another significant puzzle, and well discover an algorithm that can be implemented in nine lines of code.
 To get started, lets limit ourselves to drawing the outline of 12
cards. Use the following dimensions to get yourself started.
To get started, lets limit ourselves to drawing the outline of 12
cards. Use the following dimensions to get yourself started.
// card width and height
private int CW = 70, CH = 50;
// the left edge for each column
private int[] cardXs = { 5, 85, 165 };
// the top edge for each row
private int[] cardYs = { 5, 65, 125, 185 };
...
setSize( 240, 240 ); // canvas width and height
We've previously discussed the practice of using symbolic constants to
represent values that are likely to change.
Hard-wiring values produces weak spots in a design that are a lightning rod for change.Instructions and issues:
 The AWT Graphics class allows shapes to be drawn using the method
drawPolygon(polygonXs,polygonYs,numberOfPoints). The outline of the
three types of shapes are given below. The first row draws a
rectangle, the second row an O, and the final row an X.
The AWT Graphics class allows shapes to be drawn using the method
drawPolygon(polygonXs,polygonYs,numberOfPoints). The outline of the
three types of shapes are given below. The first row draws a
rectangle, the second row an O, and the final row an X.The X offset for each shape in one, two, and three-shape cards are also provided.
// shapes: rectangle, O, X
private int[][] shapeXs = { { 0, 16, 16, 0, 0 },
{ 0, 2, 6, 10, 14, 16, 16, 14, 10, 6, 2, 0, 0 },
{ 0, 4, 8, 12, 16, 12, 16, 12, 8, 4, 0, 4, 0 } };
private int[][] shapeYs = { { 0, 0, 37, 37, 0 },
{ 10, 3, 0, 0, 3, 10, 27, 34, 37, 37, 34, 27, 10 },
{ 4, 0, 10, 0, 4, 19, 33, 37, 28, 37, 33, 19, 4 } };
// numbers: one, two, three
private int[][] one23Xs = { { 27 }, { 17,37 }, { 7,27,47 } };
// Y margin for the top of each shape
private int SY = 6;
...
g.drawPolygon( polygonXs, polygonYs, numberOfPoints );
In this iteration, develop the code for drawing two of our four
dimensions: shape, and number. You will need to add together
contributions from several data structures to draw each shape within
each card.Instructions and issues:
 Add the last two dimensions (color and fill) in this iteration. Use
the drawPolygon(polygonXs,polygonYs,numberOfPoints) method for solid
fill. For striped fill, use the relative coordinate arrays below.
Add the last two dimensions (color and fill) in this iteration. Use
the drawPolygon(polygonXs,polygonYs,numberOfPoints) method for solid
fill. For striped fill, use the relative coordinate arrays below.
private int[][] shapeXs = {
{ 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 16, 16,
0, 16, 16, 0, 16, 16, 0, 0 },
{ 0, 2, 6, 10, 14, 2, 14, 16, 0, 16, 16, 0,
16, 16, 0, 16, 14, 2, 14, 10, 6, 2, 0, 0 },
{ 0, 4, 8, 2, 14, 8, 12, 16, 11, 16, 12, 4,
12, 16, 11, 16, 12, 8, 2, 14, 8, 4, 0, 5,
0, 4, 0, 5, 0 } };
private int[][] shapeYs = {
{ 0, 0, 6, 6, 6, 12, 12, 12, 19, 19, 19, 25,
25, 25, 31, 31, 31, 37, 37, 0 },
{ 10, 3, 0, 0, 3, 3, 3, 10, 10, 10, 19, 19, 19,
27, 27, 27, 34, 34, 34, 37, 37, 34, 27, 10 },
{ 4, 0, 11, 11, 11, 11, 0, 4, 4, 4, 19, 19, 19,
33, 33, 33, 37, 27, 27, 27, 27, 37, 33, 33,
33, 19, 4, 4, 4 } };
The fill dimension seems to be usually involved. The open fill and
striped fill use two different arrays of relative X,Y values and the
drawPolygon() instruction; while the solid fill uses the fillPolygon()
instruction and the same relative X,Y arrays as the open fill.Instructions and issues: How do you want to handle the two different sets of relative X,Y values? Do you need to keep them separate and use an if-else test to access the correct set; or, can you merge the two sets into one and compute the appropriate offset?
All permutations of four 3-value variables
|
0000 1000 2000 0100 1100 2100 0200 1200 2200 |
0010 1010 2010 0110 1110 2110 0210 1210 2210 |
0020 1020 2020 0120 1120 2120 0220 1220 2220 |
0001 1001 2001 0101 1101 2101 0201 1201 2201 |
0011 1011 2011 0111 1111 2111 0211 1211 2211 |
0021 1021 2021 0121 1121 2121 0221 1221 2221 |
0002 1002 2002 0102 1102 2102 0202 1202 2202 |
0012 1012 2012 0112 1112 2112 0212 1212 2212 |
0022 1022 2022 0122 1122 2122 0222 1222 2222 |
Instructions and issues:
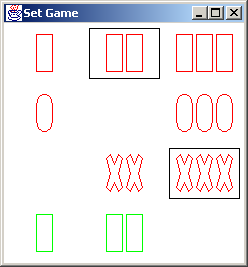
Instructions and issues:
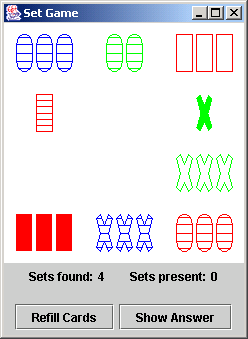
Instructions and issues:
0 0 1 1 2 2 0 0 1 2 0 1 1 2 2 0 1 0 1 2 1 1 2 2 0 0 2 0 1 2 set? no no no no no no yes yes yes yes sum 1 2 4 5 4 2 3 0 3 6 dim1 dim2 dim3 dim4 card1 0 2 1 0 card2 0 2 1 1 card3 0 2 1 2 sum 0 6 3 3 set? yes dim1 dim2 dim3 dim4 card1 0 1 2 2 card2 0 1 2 2 card3 1 2 0 1 sum 1 4 4 5 set? noInstructions and issues:
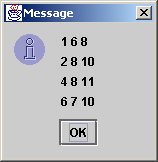
Instructions and issues:
public void paint( Graphics g ) {
for (int i=0; i < cardYs.length; i++)
for (int j=0; j < cardXs.length; j++)
g.drawRect( cardXs[j], cardYs[i], CW, CH );
}
Or - we could remove one level of bookkeeping, and use the modulus
operator and integer division to achieve the same end.
public void paint( Graphics g ) {
for (int i=0; i < 12; i++)
g.drawRect( cardXs[i%3], cardYs[i/3], CW, CH );
}
The "i%3" expression cycles through the values 0, 1, and 2. That is
exactly what the inner loop did in the previous implementation. This
could be described as a "saw-tooth function". Each time the modulus
operator jumps back to 0, the integer division expression steps to its
next level. That replaces the role of the outer loop.
Integer division is useful as a "stair-step function". The modulus operator yields a "saw-tooth function".Listing 8.1
import java.awt.*;
import javax.swing.*;
public class SetGame extends Canvas {
private int CW = 70, CH = 50;
private int[] cardXs = { 5, 85, 165 };
private int[] cardYs = { 5, 65, 125, 185 };
public static void main( String[] args ) {
new SetGame();
}
public SetGame() {
JFrame frame = new JFrame( "Set Game" );
setSize( 240, 240 );
setBackground( Color.white );
frame.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
frame.getContentPane().add( this );
frame.pack();
frame.setVisible( true );
}
public void paint( Graphics g ) {
for (int i=0; i < 12; i++)
g.drawRect( cardXs[i%3], cardYs[i/3], CW, CH );
} }
private int[] polygonXs = new int[13], polygonYs = new int[13];
...
for (int i=0; i < 9; i++) {
for (int j=0, length; j < one23Xs[i%3].length; j++) {
length = computeShapeXYs( i/3, cardXs[i%3] + one23Xs[i%3][j],
cardYs[i/3] + SY );
g.drawPolygon( polygonXs, polygonYs, length );
} }
The computeShapeXYs() function is oblivious to all the decisions being
made externally. Its sole responsibility is to iterate through the
designated shapes relative positions, and compute absolute positions.
private int computeShapeXYs( int i, int x, int y ) {
for (int j=0; j < shapeXs[i].length; j++) {
polygonXs[j] = shapeXs[i][j] + x;
polygonYs[j] = shapeYs[i][j] + y;
}
return shapeXs[i].length;
}
The notion of "overlays" put forth at the beginning of this section
reminds me of physiology textbooks that represent each sub-system of
the human body on its own clear plastic page. The skeletal system, the
circulatory system, the respiratory system, the digestive system, and
the musculature can be studied in isolation – or – they can be overlayed
and examined in concert.
In software, this kind of approach has gone by many names: divide and
conquer, separation of concerns, layers of abstraction, etc. We used
it in this iteration to: decompose the complexity of drawing shapes on
cards, and wield remarkable leverage with very little code.
Perspective is everything – separate concerns into "horizontal" layers, and at the last minute overlay them to produce a "vertical" solution.Listing 8.2
import java.awt.*;
import javax.swing.*;
public class SetGame extends Canvas {
private int CW = 70, CH = 50, SY = 6;
private int[] cardXs = { 5, 85, 165 };
private int[] cardYs = { 5, 65, 125, 185 };
private int[][] shapeXs = { { 0, 16, 16, 0, 0 },
{ 0, 2, 6, 10, 14, 16, 16, 14, 10, 6, 2, 0, 0 },
{ 0, 4, 8, 12, 16, 12, 16, 12, 8, 4, 0, 4, 0 } };
private int[][] shapeYs = { { 0, 0, 37, 37, 0 },
{ 10, 3, 0, 0, 3, 10, 27, 34, 37, 37, 34, 27, 10 },
{ 4, 0, 10, 0, 4, 19, 33, 37, 28, 37, 33, 19, 4 } };
private int[][] one23Xs = { { 27 }, { 17,37 }, { 7,27,47 } };
private int[] polygonXs = new int[13], polygonYs = new int[13];
public static void main( String[] args ) { ... }
public SetGame() { ... }
public void paint( Graphics g ) {
for (int i=0; i < 9; i++) {
g.drawRect( cardXs[i%3], cardYs[i/3], CW, CH );
for (int j=0, length; j < one23Xs[i%3].length; j++) {
length = computeShapeXYs( i/3, cardXs[i%3] + one23Xs[i%3][j],
cardYs[i/3] + SY );
g.drawPolygon( polygonXs, polygonYs, length );
} } }
private int computeShapeXYs( int i, int x, int y ) {
for (int j=0; j < shapeXs[i].length; j++) {
polygonXs[j] = shapeXs[i][j] + x;
polygonYs[j] = shapeYs[i][j] + y;
}
return shapeXs[i].length;
} }
private Color[] colors = { Color.red, Color.green, Color.blue };
...
for (int i=0; i < 9; i++) {
for (int j=0, length; j < one23Xs[i%3].length; j++) {
length = computeShapeXYs( i/3, cardXs[i%3] + one23Xs[i%3][j],
cardYs[i/3] + SY );
g.setColor( colors[i%3] );
g.drawPolygon( polygonXs, polygonYs, length );
}
For the dimension of fill, we could choose to create brand new data
structures like the following.
private int[][] shapeXs = { ... };
private int[][] shapeYs = { ... };
private int[][] stripeXs = {
{ 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 0 }, ... };
private int[][] stripeYs = {
{ 0, 0, 6, 6, 6, 12, 12, 12, 19, 19, 19, 25, 25, 25, 31, 31, 31, 37, 37, 0 }, ... };
The fill dimension needs to cycle in step with the number and color
dimensions, so the expression "i%3" will be necessary to compute array
indices. When "i%3" is equal to 0, the fill should be open. When "i%3" is
1, the fill is striped. And "i%3" equal to 2 means a fill of solid.
Since the fill affects how the polygon Xs and Ys are computed, the
method computeShapeXYs() will need to change.
private int computeShapeXYs( int i, int x, int y ) {
if (i%3 == 1) {
for (int j=0; j < stripeXs[i].length; j++) {
polygonXs[j] = stripeXs[i][j] + x;
polygonYs[j] = stripeYs[i][j] + y;
}
return stripeXs[i].length;
} else {
for (int j=0; j < shapeXs[i].length; j++) {
polygonXs[j] = shapeXs[i][j] + x;
polygonYs[j] = shapeYs[i][j] + y;
}
return shapeXs[i].length;
} }
asd
private int[][] shapeXs = { openRect, openO, openX, stripedRect, stripedO, stripedX };
public void paint( Graphics g ) {
for (int i=0; ... ) {
...
for (int j=0, ... ) {
length = computeShapeXYs( i, ... );
...
} } }
private int computeShapeXYs( int i, int x, int y ) {
int shapeIndex = i/3 + (3 * (i%3 == 1 ? 1 : 0));
for (int j=0; j < shapeXs[shapeIndex].length; j++) {
polygonXs[j] = shapeXs[shapeIndex][j] + x;
polygonYs[j] = shapeYs[shapeIndex][j] + y;
}
return shapeXs[shapeIndex].length;
}
asd
private int[][] shapeXs = { openRect, stripedRect, openO, stripedO, openX, stripedX };
private int computeShapeXYs( int i, int x, int y ) {
int shapeIndex = i/3 * 2 + (i%3 == 1 ? 1 : 0);
...
The method paint() needs to decide whether to invoke drawPolygon() or
fillPolygon().
public void paint( Graphics g ) {
...
g.setColor( colors[i%3] );
if (i%3 == 2)
g.fillPolygon( polygonXs, polygonYs, length );
else
g.drawPolygon( polygonXs, polygonYs, length );
} }
Listing 8.3
import java.awt.*;
import javax.swing.*;
public class SetGame extends Canvas {
private int CW = 70, CH = 50, SY = 6;
private int[] cardXs = { 5, 85, 165 };
private int[] cardYs = { 5, 65, 125, 185 };
private int[][] shapeXs = { { 0, 16, 16, 0, 0 },
{ 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 16, 16, 0, 0 },
{ 0, 2, 6, 10, 14, 16, 16, 14, 10, 6, 2, 0, 0 },
{ 0, 2, 6, 10, 14, 2, 14, 16, 0, 16, 16, 0, 16, 16, 0, 16, 14, 2, 14, 10,
6, 2, 0, 0 },
{ 0, 4, 8, 12, 16, 12, 16, 12, 8, 4, 0, 4, 0 },
{ 0, 4, 8, 2, 14, 8, 12, 16, 11, 16, 12, 4, 12, 16, 11, 16, 12, 8, 2, 14,
8, 4, 0, 5, 0, 4, 0, 5, 0 } };
private int[][] shapeYs = { { 0, 0, 37, 37, 0 },
{ 0, 0, 6, 6, 6, 12, 12, 12, 19, 19, 19, 25, 25, 25, 31, 31, 31, 37, 37, 0 },
{ 10, 3, 0, 0, 3, 10, 27, 34, 37, 37, 34, 27, 10 },
{ 10, 3, 0, 0, 3, 3, 3, 10, 10, 10, 19, 19, 19, 27, 27, 27, 34, 34, 34, 37,
37, 34, 27, 10 },
{ 4, 0, 10, 0, 4, 19, 33, 37, 28, 37, 33, 19, 4 },
{ 4, 0, 11, 11, 11, 11, 0, 4, 4, 4, 19, 19, 19, 33, 33, 33, 37, 27, 27,
27, 27, 37, 33, 33, 33, 19, 4, 4, 4 } };
private int[][] one23Xs = { { 27 }, { 17,37 }, { 7,27,47 } };
private int[] polygonXs = new int[29], polygonYs = new int[29];
private Color[] colors = { Color.red, Color.green, Color.blue };
public static void main( String[] args ) { ... }
public SetGame() { ... }
public void paint( Graphics g ) {
for (int i=0; i < 9; i++) {
g.setColor( Color.black );
g.drawRect( cardXs[i%3], cardYs[i/3], CW, CH );
for (int j=0, length; j < one23Xs[i%3].length; j++) {
length = computeShapeXYs( i, cardXs[i%3] + one23Xs[i%3][j],
cardYs[i/3] + SY );
g.setColor( colors[i%3] );
if (i%3 == 2)
g.fillPolygon( polygonXs, polygonYs, length );
else
g.drawPolygon( polygonXs, polygonYs, length );
} } }
private int computeShapeXYs( int i, int x, int y ) {
int shapeIndex = i/3 * 2 + (i%3 == 1 ? 1 : 0);
for (int j=0; j < shapeXs[shapeIndex].length; j++) {
polygonXs[j] = shapeXs[shapeIndex][j] + x;
polygonYs[j] = shapeYs[shapeIndex][j] + y;
}
return shapeXs[shapeIndex].length;
} }
Listing 8.4
as
Listing 8.5
as
Listing 8.6
as
Listing 8.7
as
The problem at hand is: how to decide (or compute) whether any arbitrary combination of three Card objects (i.e. three entries from table 2) represent a set. One approach could be to loop through each of the three dimensions, and examine the corresponding digits for each dimension on all three Cards.
To this end, let's enumerate all combinations of the digits 0, 1, and 2 (leaving out all permutations that represent different orderings of the same data). The result would be table 3. The "012" column represents a "different" set; and the "000", "111", "222" columns are "same" sets. The first six columns of digits do not represent sets.
On a hunch, let's try adding each column. All the columns that represent sets are found to be evenly divisible by three. All the columns that don't represent sets are not. That is a remarkable property that significantly simplifies the evaluation of "set-hood".
Given this special "modulus" property, the implementation of the isValid() method is easy. An outer loop can iterate over the number of facets in our domain, and an inner loop can iterate over the number of Cards in a set. If the sum of any of the facets is not evenly divisible by three, then the current combination cannot be a set.
Listing 8.8
Listing 8.9