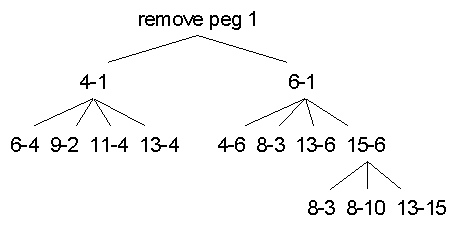


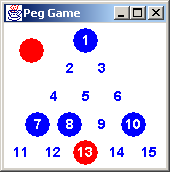
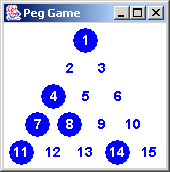
 It would be nice if our Peg Game application could keep the player from
painting herself into a corner. Take the board to the right. The
correct sequence of moves are: 7 to 9, 13 to 6, 10 to 3, and 1 to 6.
If the player chooses 13 to 4 instead; then 7 can jump to 2, and 1 to
4. That would result in two pegs remaining: 4 and 10. So, our game
needs to sound an alarm (e.g. draw a red dot) when the user asks for
the 13 to 4 move.
It would be nice if our Peg Game application could keep the player from
painting herself into a corner. Take the board to the right. The
correct sequence of moves are: 7 to 9, 13 to 6, 10 to 3, and 1 to 6.
If the player chooses 13 to 4 instead; then 7 can jump to 2, and 1 to
4. That would result in two pegs remaining: 4 and 10. So, our game
needs to sound an alarm (e.g. draw a red dot) when the user asks for
the 13 to 4 move.Other interesting activities would include questions like:
Three iterations:
1 4-1 11-4 9-2 12-5 14-12 2-7 3-8 7-9 10-3 1-6 6-13 12-14 15-13 1 6-1 8-3 15-6 14-5 2-9 7-2 3-10 10-8 1-4 12-14 4-13 14-12 11-13 ... 4 1-4 7-2 13-4 10-8 3-10 11-13 14-12 4-13 13-11 15-6 6-4 2-7 11-4 4 6-4 12-5 4-6 10-8 3-10 11-4 15-6 14-12 2-7 12-5 6-4 7-2 1-4 4 11-4 13-11 6-13 2-7 1-6 11-4 14-12 10-3 4-6 3-10 12-5 15-6 6-4 4 13-4 10-8 15-13 12-14 4-13 14-12 1-4 3-10 7-2 2-9 10-8 11-13 13-4 ... total solutions found - 250The initial hole position is listed first, followed by the 13 moves. Do not report duplicate moves. Sort the output before presenting it.
For this iteration, lets be exceedingly simple-minded. Randomly pick an initial hole position, and then randomly pick one random move after another.
Instructions and issues:
> java PegGameSolve 1 6-1 13-6 10-3 11-13 14-12 4-13 1-4 7-2 12-14 15-13 3-8 13-4 2-7 6-1 13-6 10-3 4-6 11-13 1-4 14-12 7-2 12-5 2-9 3-10 15-6 6-13 ... total solutions for hole at 1 is 29760 total tries was 568630, 1 out of 19 attempts successful > java PegGameSolve 2 7-2 13-4 15-13 3-8 12-14 10-3 1-6 6-13 14-12 11-13 2-7 13-4 4-11 7-2 13-4 15-13 2-7 3-8 10-3 12-5 13-6 3-10 11-4 4-6 10-3 1-6 ... total solutions for hole at 2 is 14880 total tries was 294543, 1 out of 19 attempts successful > java PegGameSolve 4 13-4 11-13 14-12 10-8 4-13 3-10 1-4 7-2 2-9 15-6 12-14 6-13 14-12 13-4 11-13 14-12 6-13 12-14 2-9 7-2 15-6 3-10 1-4 14-5 4-6 6-15 ... total solutions for hole at 4 is 85258 total tries was 1149568, 1 out of 13 attempts successful > java PegGameSolve 5 12-5 14-12 6-13 2-9 15-6 12-14 7-2 3-10 1-4 10-8 4-13 14-12 11-13 total solutions for hole at 5 is 1550 total tries was 137846, 1 out of 88 attempts successfulHow can you algorithmically enumerate and test every possible pathway through the game? How do people do it when they play the game? A person could write down each move taken, and then when a dead-end is reached, backtrack one of more moves, and make a different choice.
A more methodical approach would be to create a tree that records all possible moves as the state of the game advances. Solutions are then found by identifying traversals of the tree that are 13 moves long (you start with 14 pegs and end with 1).




Here is an alternate representation that demonstrates four non-solutions. After 7 moves, the board has reached the state shown at the top. Four moves are now possible. If the 3-8 move is chosen, then two moves are possible. The 13-4 move eventually leads to three pegs remaining, and the 1-4 move leads to an end state of five pegs.
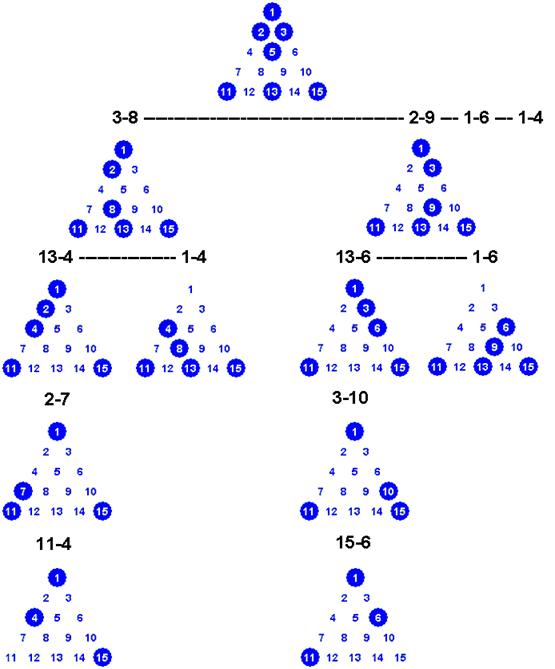
A graphical representation is optimal for carbon-based intelligence (i.e. people), but it doesnt map directly to silicon-based intelligence (computers). If we had a representation that was more sequential in nature (like a computers memory), then we could perhaps kill two birds with one stone: discuss a solution strategy for the problem, and, lay the foundation for the eventual algorithm.
Another issue with the graphical representation above is overhead. Modeling all the possible moves of a game as separate nodes in a fully populated tree consumes a lot of memory. As we come up with a more sequential encoding of the game, is there a way we could accommodate some kind of just in time representation? The motivation is to maintain as little game state as possible.
Instead of building a full-grown tree, perhaps a step-by-step list of lists representation will provide sufficient bookkeepping for: testing one specific game, backtracking to alternate games, and ultimately testing every possible game. How about the following procedure and data structure?
remove peg 1 (4-1 6-1) (4-1 (4-6 8-3 13-6 15-6) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 8-3) ) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 (3-10 13-15 14-5) ) ) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 (3-10 13-15 (3-8 3-10 12-14 2-9) ) ) ) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 (3-10 13-15 (3-8 3-10 12-14 (3-10 7-2 12-14) ) ) ) ) )The board now looks like -

To eliminate some clutter, let's focus only on the last list of moves. The steps remain: move, generate, replace.
(3-10 7-2 12-14) 9 pegs left (3-10 7-2 (6-13 7-2 14-5 3-10) ) 8 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 10-8) ) ) 7 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 7-9) ) ) ) 6 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 (14-5) ) ) ) ) 5 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 ((4-6)) ) ) ) ) 4 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 (( )) ) ) ) ) 3 pegs leftAt this point, the pegs remaining are 1, 6, 11; and there are no more possible moves.
We've hit a dead-end, and need to backtrack to an alternate pathway. Lets add a new step 3 to our procedure.
The top line below looks like the fourth line above - except - the 7-9 move at the end has been removed. We are ready to proceed forward again. As each last move of the last list is executed, there is only one possible move on the board. So, each replacement is performed with a list composed of a single move.
(3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2) ) ) ) 6 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 ((1-4)) ) ) ) 5 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (((4-13))) ) ) ) 4 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 ((((14-12)))) ) ) ) 3 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (((((11-13))))) ) ) ) 2 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 ((((())))) ) ) ) 1 peg left
We now have a "sequential" representation of our puzzle. It should give us a good start on a search algorithm. Notice how the list demonstrates last in, first out behavior.
Our 4-step procedure seems to suggest a loop where step 4 feeds back to step 2. Would recursion be more, or less, useful?
Instructions and issues:
<A>
<B> <C>
<D> <E> f
g h <I> j
<K> l <M> <N> <O>
Move (from to): c e
NOT A LEGAL MOVE
<A>
<B> <C>
<D> <E> f
g h <I> j
<K> l <M> <N> <O>
Move (from to): c h
NOT A GOOD IDEA - TRY A BETTER MOVE
|

|
attemptMove() to return something that indicates a bad move.
depthFirstSearch() to return as soon as the first solution is
found.
List solutions = new ArrayList(); ... if ( ! solutions.contains( sb.toString() )) solutions.add( sb.toString() ); ... Object[] array = solutions.toArray(); Arrays.sort( array ); for (int i=0; i < array.length; i++) System.out.println( array[i] );The
TreeSet class is a very useful component. It is a collection
resource that enforces a single instance of each contained object. If
the user attempts to add the same solution string more than once, all
subsequent add requests simply overwrite the original string. This
property will allow us to screen out all duplicate solutions. Another
useful property of TreeSet is that it maintains its elements in sorted
order.
private static List moveList = new ArrayList(); // a "global" variable
public static void main( String[] args ) {
int gameCount = 0;
Set solutions = new TreeSet();
StringBuffer sb = new StringBuffer();
while (true) {
reset();
pickHole();
while (findMove())
;
gameCount++;
if (pegCount == 1) {
sb.setLength( 0 );
for (int i=0; i < moveList.size(); i++) {
sb.append( moveList.get(i) );
sb.append( " " );
}
solutions.add( sb.toString() );
}
if (gameCount == 50000)
break;
}
...
Once the main processing loop has completed, the solutions object can
be examined by using the standard idiom for traversing all Java
collection classes.
for (Iterator it = solutions.iterator(); it.hasNext(); ) System.out.println( it.next() ); System.out.println( "total solutions found - " + solutions.size() );The
pickHole() function above simply picks a random number between 0
and 15. The findMove() function is more interesting. The jumpTable
data structure provides remarkable leverage with its linear
representation of all candidate moves. We can use a random number to
grab random moves. For the sake of efficiency, if we havent found a
move after 15 tries, then resort to brute force and search the array
from beginning to end.
We've seen the legalMove() function in previous chapters. What has been
added here is storing each legal move in the moveList data structure.
private static boolean findMove() {
for (int i=0, num; i < 15; i++) {
num = rn.nextInt( jumpTable.length );
if (legalMove( num ))
return true;
}
for (int i=0; i < jumpTable.length; i++)
if (legalMove( i ))
return true;
return false;
}
private static boolean legalMove( int n ) {
if (pegsPresent[ jumpTable[n][0]-1 ] … ) {
...
moveList.add( "" + jumpTable[n][0] + "-" + jumpTable[n][1] );
return true;
}
return false;
}
Running the program in listing 6.1 many times produced a total number
of solutions ranging from 231 to 288. Its amazing how hard it is for a
person to find just one solution! Another interesting observation is:
the initial hole can start in any position and the game can still be
won.If these questions were all we were interested in, this solution would be entirely sufficient. Depending on the projects requirements, a quick-and-dirty solution using random moves and sheer brute force could be more desirable than a vigorous solution.
Start stupid and evolve. [Kent Beck]Listing 6.1
import java.util.*;
import java.io.*;
public class PegGameSolveRandom {
// "global" variables - used in one or more functions
private static Random rn = new Random();
private static boolean[] pegsPresent = new boolean[15];
private static List moveList = new ArrayList();
private static int pegCount;
private static int jumpTable[][] = { {1,4,2}, ... , {15,6,10} };
private static void reset() {
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
moveList.clear();
pegCount = pegsPresent.length;
}
private static void pickHole() {
int num = rn.nextInt( pegsPresent.length );
pegsPresent[num] = false;
moveList.add( (num < 9 ? " " : "") + (num+1) );
pegCount--;
}
private static boolean findMove() {
for (int i=0, num; i < 15; i++) {
num = rn.nextInt( jumpTable.length );
if (legalMove( num ))
return true;
}
for (int i=0; i < jumpTable.length; i++)
if (legalMove( i ))
return true;
return false;
}
private static boolean legalMove( int n ) {
if (pegsPresent[ jumpTable[n][0]-1 ] // if "from" position is filled
&& pegsPresent[ jumpTable[n][2]-1 ] // if "jumped" posit is filled
&& ( ! pegsPresent[ jumpTable[n][1]-1 ])) { // if "to" position is vacant
pegsPresent[ jumpTable[n][0]-1 ] = false;
pegsPresent[ jumpTable[n][2]-1 ] = false;
pegsPresent[ jumpTable[n][1]-1 ] = true;
pegCount--;
moveList.add( "" + jumpTable[n][0] + "-" + jumpTable[n][1] );
return true;
}
return false;
}
public static void main( String[] args ) {
int gameCount = 0;
Set solutions = new TreeSet();
StringBuffer sb = new StringBuffer();
while (true) {
reset();
pickHole();
while (findMove())
;
gameCount++;
if (pegCount == 1) {
sb.setLength( 0 );
for (int i=0; i < moveList.size(); i++) {
sb.append( moveList.get(i) );
sb.append( " " );
}
solutions.add( sb.toString() );
}
if (gameCount == 50000)
break;
}
for (Iterator it = solutions.iterator(); it.hasNext(); )
System.out.println( it.next() );
System.out.println( "total solutions found - " + solutions.size() );
} }
depthFirstSearch().Another indicator for the appropriateness of recursion is nested data. Our list data structure may contain any combination of atomic moves, or other lists. The definition of a list inextricably refers to itself.
Consider using recursion when the data contains instances of itself (i.e. is recursively-defined).Finding all currently available moves is a simple matter of trying every move in the jumpTable data structure. Well append each move found to the end of an
ArrayList attribute. Distinguishing each lower
level list from its parent can be accomplished by remembering the
number of sibling elements at each level. That knowledge is initiated
by returning the number of moves pushed on the deferredMoveStack by the
pushPossibleMovesOnDeferredMoveStack() methods.
public PegGameSolveSearch( int hole ) {
...
int numPushed = pushPossibleMovesOnDeferredMoveStack();
for (int j=0; j < numPushed; j++)
depthFirstSearch(); }
private List deferredMoveStack = new ArrayList();
private int pushPossibleMovesOnDeferredMoveStack() {
int numPushed = 0;
for (int i=0; i < jumpTable.length; i++)
if (possibleMove( i )) {
deferredMoveStack.add( 0, new Integer(i) );
numPushed++;
}
return numPushed;
}
private boolean possibleMove( int n ) {
if (pegsPresent[ jumpTable[n][0]-1 ] … )
return true;
return false;
}
The last move pushed to the deferredMoveStack should be the first move
removed and executed. Every recursive function needs a test to
determine if recursion should stop. The recursion in
depthFirstSearch() should not proceed in two situations: when there is
a single peg left on the board, or, when all the moves pushed by
pushPossibleMovesOnDeferredMoveStack() have been exhausted.
Because we want to traverse all possible pathways through the game; as
the algorithm reverses itself in anticipation of processing unexplored
sub-trees, the move done at the beginning of depthFirstSearch() must be
undone.
The total number of games attempted can be computed by counting the
number of leaf nodes in a tree representation like that at the start of
this chapter. Leaf nodes represent solutions (one peg remaining) and
dead-ends. If pushPossibleMovesOnDeferredMoveStack() identified one or
more possible moves, that situation would represent an interior node in
the tree, and should not be counted.
private void depthFirstSearch() {
int i = ((Integer)deferredMoveStack.remove( 0 )).intValue();
doMove( i );
if (pegCount == 1) {
report();
totalTries++;
undoMove( i );
return;
}
int numPushed = pushPossibleMovesOnDeferredMoveStack();
for (int j=0; j < numPushed; j++)
depthFirstSearch();
if (numPushed == 0) totalTries++;
undoMove( i );
}
The "magic" in this program resides in the depthFirstSearch() method.
What remains to be discussed is a little housekeeping. As moves are
done, they are remembered in a queue called currentMoveList. When they
are "undone", they are removed from the queue. When a solution is found,
the queue is traversed, and the sequence of moves reported to a file
and to standard out.
private List currentMoveList = new ArrayList();
private void doMove( int n ) {
pegsPresent[ jumpTable[n][0]-1 ] = false;
pegsPresent[ jumpTable[n][2]-1 ] = false;
pegsPresent[ jumpTable[n][1]-1 ] = true;
pegCount--;
currentMoveList.add( new Integer(n) );
}
private void undoMove( int n ) {
pegsPresent[ jumpTable[n][0]-1 ] = true;
pegsPresent[ jumpTable[n][2]-1 ] = true;
pegsPresent[ jumpTable[n][1]-1 ] = false;
pegCount++;
currentMoveList.remove( currentMoveList.size()-1 );
}
private void report() {
for (int i=0, n; i < currentMoveList.size(); i++) {
...
Let's consider questions that were asked at the beginning of this
chapter:
total solutions for hole at 1 is 29760 total tries was 568630, 1 out of 19 attempts successful total solutions for hole at 2 is 14880 total tries was 294543, 1 out of 19 attempts successful total solutions for hole at 4 is 85258 total tries was 1149568, 1 out of 13 attempts successful total solutions for hole at 5 is 1550 total tries was 137846, 1 out of 88 attempts successfulWe can easily confirm our symmetry assumption by specifying the initial hole positions of interest.
total solutions for hole at 5 is 1550 total tries was 137846, 1 out of 88 attempts successful total solutions for hole at 8 is 1550 total tries was 137846, 1 out of 88 attempts successful total solutions for hole at 9 is 1550 total tries was 137846, 1 out of 88 attempts successfulThe exterior middle positions can be utilized by twice as many moves as the other types of positions (they support four jumps, while the other position types only support two). Intuition might suggest that they should yield twice as many solutions. This is not the case. Intuition might also speculate that the interior peg positions are no less likely to yield a solution than their neighbors. And again, this is not true.
Intuition is serviceable for everything, sufficient for nothing. [Adaptation of a quote from Henri-Frederic Amiel]Listing 6.2
import java.util.*;
import java.io.*;
public class PegGameSolveSearch {
private boolean[] pegsPresent = new boolean[15];
private List deferredMoveStack = new ArrayList();
private List currentMoveList = new ArrayList();
private int pegCount;
private static int totalSolutions, totalTries;
private static FileWriter fw;
public PegGameSolveSearch( int hole ) {
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
pegsPresent[hole] = false;
pegCount = pegsPresent.length - 1;
int numPushed = pushPossibleMovesOnDeferredMoveStack();
for (int j=0; j < numPushed; j++)
depthFirstSearch();
}
private void depthFirstSearch() {
int i = ((Integer)deferredMoveStack.remove( 0 )).intValue();
doMove( i );
if (pegCount == 1) {
report();
totalTries++;
undoMove( i );
return;
}
int numPushed = pushPossibleMovesOnDeferredMoveStack();
for (int j=0; j < numPushed; j++)
depthFirstSearch();
if (numPushed == 0) totalTries++;
undoMove( i );
}
private int pushPossibleMovesOnDeferredMoveStack() {
int numPushed = 0;
for (int i=0; i < jumpTable.length; i++)
if (possibleMove( i )) {
deferredMoveStack.add( 0, new Integer(i) );
numPushed++;
}
return numPushed;
}
private boolean possibleMove( int n ) {
if (pegsPresent[ jumpTable[n][0]-1 ] // if "from" position is filled
&& pegsPresent[ jumpTable[n][2]-1 ] // if "jumped" position is filled
&& ( ! pegsPresent[ jumpTable[n][1]-1 ])) // if "to" position is vacant
return true;
return false;
}
private void doMove( int n ) {
pegsPresent[ jumpTable[n][0]-1 ] = false;
pegsPresent[ jumpTable[n][2]-1 ] = false;
pegsPresent[ jumpTable[n][1]-1 ] = true;
pegCount--;
currentMoveList.add( new Integer(n) );
}
private void undoMove( int n ) {
pegsPresent[ jumpTable[n][0]-1 ] = true;
pegsPresent[ jumpTable[n][2]-1 ] = true;
pegsPresent[ jumpTable[n][1]-1 ] = false;
pegCount++;
currentMoveList.remove( currentMoveList.size()-1 );
}
private void report() {
totalSolutions++;
try {
for (int i=0, n; i < currentMoveList.size(); i++) {
n = ((Integer)currentMoveList.get( i )).intValue();
if (totalSolutions % 1000 == 0)
System.out.print( prt(n) + " " );
fw.write( prt(n) + " " );
}
if (totalSolutions % 1000 == 0)
System.out.println();
fw.write( "\r\n" );
} catch (IOException ex) { ex.printStackTrace(); }
}
private String prt( int n ) {
return "" + jumpTable[n][0] + "-" + jumpTable[n][1];
}
public static void main( String[] args ) {
try {
fw = new FileWriter( "PegGameSolve.out" );
} catch (IOException ex) { ex.printStackTrace(); }
int hole = Integer.parseInt( args[0] );
new PegGameSolveSearch( hole-1 );
System.out.println( "totalSolutions for hole at " +hole+ " is " + totalSolutions );
System.out.println( "totalTries was " + totalTries + ", 1 out of "
+ (totalTries/totalSolutions) );
try {
fw.write( "totalSolutions for hole at " +hole+ " is " + totalSolutions + "\r\n" );
fw.close();
} catch (IOException ex) { ex.printStackTrace(); }
}
private static int jumpTable[][] = { {1,4,2}, ... , {15,6,10} };
}
A good place to start is where the view asks the model to attemptMove(). The model will compute if the requested move has a successful future, and the view needs to know if the requested move is destined to fail. Lets change the return type of attemptMove() from void to String. The value of the returned string can then be displayed directly by the DOS view.
Move (from to): c h NOT A GOOD IDEA - TRY A BETTER MOVE Move (from to): a b NOT A LEGAL MOVEThe code that processed the jumpTable data structure has been put in its own method -
legalMove().
The requested move needs to be executed before a determination can be
made on whether the success of the game is at risk. The code that
manipulated the model's pegsPresent data structure has been encapsulated
in a new method called doMove().
We are now ready to test if: the game has been won, or the game is
capable of being won. For the former, the pegCount attribute was
added. For the latter, the aSolutionIsPossible() method was created.
For now, lets believe that this method is capable of unadulterated
magic returning true if a solution is possible, and false otherwise.
Any sufficiently refined abstraction is indistinguishable from magic. [Variation on Clarke's Third Law: "Any sufficiently advanced technology is indistinguishable from magic."]If the requested move is valid and good, there is no error message to return to the view, so return null. Otherwise, the move needs to be undone, and the user needs to be politely slapped on the wrist.
public String attemptMove( int from, int to ) {
int i;
if ((i = legalMove( from, to )) == -1)
return "NOT A LEGAL MOVE";
doMove( i );
if (pegCount == 1 || aSolutionIsPossible()) {
view.setPeg( jumpTable[i][0]-1, false);
view.setPeg( jumpTable[i][2]-1, false);
view.setPeg( jumpTable[i][1]-1, true);
return null;
}
undoMove( i );
return "NOT A GOOD IDEA - TRY A BETTER MOVE";
}
Lets return to the aSolutionIsPossible() method. It needs to return
true if a solution is possible, and false otherwise. The attemptMove()
method has already executed the requested move, so we are ready to
identify the list of possible moves and launch the recursive search
algorithm. This method is basically the constructor from the
PegGameSolveSearch program.
Unlike the program in the last chapter, we are only interested in the
first solution found - not trying to collect all possible solutions.
As a result, depthFirstSearch() has been modified to return true or
false as appropriate. This method needs the deferredMoveStack data
structure, and that stack needs to be emptied out before
aSolutionIsPossible() is called the next time.
private ArrayList deferredMoveStack = new ArrayList();
private boolean aSolutionIsPossible() {
boolean result = false;
int numPushed = pushPossibleMovesOnDeferredMoveStack();
for (int j=0; j < numPushed; j++)
if ((result = depthFirstSearch()) == true)
break;
deferredMoveStack.clear();
return result;
}
The "magic" method - depthFirstSearch() - changes very little. When a
solution is found, it needs to return true immediately. Otherwise,
false is returned. In the for loop, whenever a recursive invocation of
itself returns, one of two things has happened: a solution was found,
or a dead-end was found. Regardless, the current invocation of the
method should immediately clean-up and return.
private boolean depthFirstSearch() {
int i = ((Integer)deferredMoveStack.remove( 0 )).intValue();
doMove( i );
if (pegCount == 1) {
undoMove( i );
return true;
}
int numPushed = pushPossibleMovesOnDeferredMoveStack();
for (int j=0; j < numPushed; j++)
if (depthFirstSearch()) {
undoMove( i );
return true;
}
undoMove( i );
return false;
}
The pushPossibleMovesOnDeferredMoveStack() and possibleMove() methods
from the previous chapter can be copied with no changes. The
currentMoveList data structure is no longer needed,
so the doMove() and
undoMove() methods no longer need to update it.
The signature of the attemptMove() method has changed - so - both views
need to be adapted. The DOS view needs to accept the string returned
from the model and print it to standard out if it is not null.
String input, message = null;
...
while (true) {
if (message != null)
System.out.println( "\n" + message );
...
message = model.attemptMove( from, to );
}
In the Swing view, when a non-null string is returned by attemptMove(),
a red dot needs to be thrown in the users face. The actual drawing
could be done in the mousePressed() method, but what would happen if
the Peg Game window is covered with another window, and then
uncovered? The only part of the user interface that is reinstated is
that which is drawn in the paint() method.
So, lets try this: add a new attribute (boolean redFlag), set it in
mousePressed(), and get it in paint(). Because of the additional user
interface wrinkle introduced by the red dot, life would be simpler if
we removed all the drawPeg() calls in mousePressed(), and added a
single repaint() call at the bottom.
private boolean redFlag;
public void mousePressed( MouseEvent e ) {
...
redFlag = false;
if (firstPeg == -2) { // initial state - select starting hole
pegsPresent[i] = false;
// drawPeg( i, g );
model.removePeg( i );
firstPeg = -1;
} else if (firstPeg == -1) { // select source peg
firstPeg = i;
// drawPeg( i, g );
} else if (firstPeg == i) { // unselect source peg
firstPeg = -1;
// drawPeg( i, g );
} else { // select destination hole
String str = model.attemptMove( firstPeg, i );
if (str != null)
redFlag = true;
else
firstPeg = -1;
}
repaint();
}
public void paint( Graphics g ) {
for (int i=0; i < pegsPresent.length; i++)
drawPeg( i, g );
if (redFlag) {
g.setColor( Color.red );
g.fillOval( 15, 15, 25, 25 );
} }
Listing 6.3
import java.util.ArrayList;
class PegGameModel {
private PegGameView view;
private boolean[] pegsPresent = new boolean[15];
private int pegCount = pegsPresent.length;
private ArrayList deferredMoveStack = new ArrayList();
public PegGameModel( PegGameView v ) {
view = v;
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
}
public void removePeg( int i ) {
pegsPresent[i] = false;
pegCount--;
}
public String attemptMove( int from, int to ) {
int i;
if ((i = legalMove( from, to )) == -1)
return "NOT A LEGAL MOVE";
doMove( i );
if (pegCount == 1 || aSolutionIsPossible()) {
view.setPeg( jumpTable[i][0]-1, false);
view.setPeg( jumpTable[i][2]-1, false);
view.setPeg( jumpTable[i][1]-1, true);
return null;
}
undoMove( i );
return "NOT A GOOD IDEA - TRY A BETTER MOVE";
}
private int legalMove( int one, int two ) {
one++; two++;
for (int i=0; i < jumpTable.length; i++)
if (one == jumpTable[i][0] && two == jumpTable[i][1]
&& pegsPresent[ jumpTable[i][0]-1 ] // if sourcePeg is present
&& pegsPresent[ jumpTable[i][2]-1 ] // if jumpedPeg is present
&& ( ! pegsPresent[ jumpTable[i][1]-1 ])) // if destination is empty
return i;
return -1;
}
private boolean aSolutionIsPossible() {
int numPushed = pushPossibleMovesOnDeferredMoveStack();
boolean result = false;
for (int j=0; j < numPushed; j++)
if ((result = depthFirstSearch()) == true)
break;
deferredMoveStack.clear();
return result;
}
private int pushPossibleMovesOnDeferredMoveStack() {
int numPushed = 0;
for (int i=0; i < jumpTable.length; i++)
if (possibleMove( i )) {
deferredMoveStack.add( 0, new Integer(i) );
numPushed++;
}
return numPushed;
}
private boolean possibleMove( int n ) {
if (pegsPresent[ jumpTable[n][0]-1 ] // if sourcePeg is present
&& pegsPresent[ jumpTable[n][2]-1 ] // if jumpedPeg is present
&& ( ! pegsPresent[ jumpTable[n][1]-1 ])) // if destination is empty
return true;
return false;
}
private void doMove( int n ) {
pegsPresent[ jumpTable[n][0]-1 ] = false; // sourcePeg
pegsPresent[ jumpTable[n][2]-1 ] = false; // jumpedPeg
pegsPresent[ jumpTable[n][1]-1 ] = true; // destination
pegCount--;
}
private void undoMove( int n ) {
pegsPresent[ jumpTable[n][0]-1 ] = true;
pegsPresent[ jumpTable[n][2]-1 ] = true;
pegsPresent[ jumpTable[n][1]-1 ] = false;
pegCount++;
}
private boolean depthFirstSearch() {
int i = ((Integer)deferredMoveStack.remove( 0 )).intValue();
doMove( i );
if (pegCount == 1) {
undoMove( i );
return true;
}
int numPushed = pushPossibleMovesOnDeferredMoveStack();
for (int j=0; j < numPushed; j++)
if (depthFirstSearch()) {
undoMove( i );
return true;
}
undoMove( i );
return false;
}
private int jumpTable[][] = { {1,4,2}, ... , {15,6,10} };
}