Three iterations:
Instructions and issues:
Instructions and issues:
How do you want to divvy up the current code base? What state exists in our application? Should any state be replicated (or cached) in each view for the sake of efficiency or simplicity? Which functions represent functionality that is independent of user interface, and which functions are peculiar to the DOS or GUI interfaces? What method signatures are sufficient to establish a contract between the cornerstone model and all optional views?
Instructions and issues:
JFrame frame = new JFrame( "Peg Game" );
frame.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
frame.getContentPane().setLayout( new GridLayout( 5,1 ) );
JPanel panel;
JRadioButton peg;
for (int row=0; row < 5; row++) {
panel = new JPanel();
panel.setBackground( Color.white );
frame.getContentPane().add( panel );
for (int column=0; column <= row; column++) {
panel.add( peg = new JRadioButton( " ", true ) );
peg.setBackground( Color.white );
} }
frame.pack();
frame.setVisible( true );
In order to draw graphics primitives, and capture mouse input, a Canvas
component is used. There are any number of ways that classes can be
specialized, methods overridden, and components configured; but having
PegGameSwing extend the Canvas class and then add itself to the
BorderLayout manager of the frame's content pane minimizes the number
of objects created.
public class PegGameSwing extends Canvas {
...
frame.getContentPane().add( this );
The Canvas component provides a paint() method that must be overridden
to initially draw the canvas' display, and, redraw the canvas as
portions are exposed when windows are moved resized. Redrawing the
entire board each time an expose event is generated does not optimize
performance, but we are primarily interested in more generic algorithm
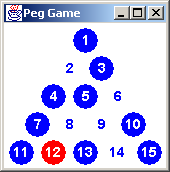
and data structure subjects.To draw 15 ovals in the game's triangular shape, we have the choice to "compute or store" the X and Y positions of each. The choice made in listing 5.1 was to store those values. The reason was that it seems to be more self-documenting. The reader can readily browse the adjacent entries, and infer "the method behind the madness".
Rather than hard-coding literal constants throughout the code, life is always made easier by introducing an "extra level of indirection" with symbolic constants. When the inevitable happens, and change occurs, having these kinds of values defined in only one place makes it very easy to change their values.
The array of Y values is easy. Each row is drawn at a constant Y value. That value need only be replicated the correct number of times per row. The array of X values is more subtle. Looking at the left edges of the 15 pegs, we see there are nine different X values. The 11 peg is drawn at the first X value, 7 peg at the second, 4 and 12 pegs at the third, 2 and 8 pegs at the fourth, 1/5/13 pegs at the fifth, 3 and 9 pegs at the sixth, 6 and 14 pegs at the seventh, 10 peg at the eighth, 15 peg at the ninth.
Drawing the label for each peg is more interesting. The expression ""+(i+1) is a cheap way to convert an integer to a string. Labels 1 through 9 are narrower than labels 10 through 15, and need to be drawn further to the right. We could use the ternary operator to explicitly choose which XS array element to use. Listing 5.1 uses integer division instead. This operator throws away the remainder of the division (precisely the thing that the modulus operator returns). The expression below returns 0 for values 0 through 8, and 1 for values 9 through 14.
private static final int[] XS = { 9, 4 };
...
g.drawString( "" + (i+1), X[i] + ((i < 9) ? XS[0] : XS[1]), Y[i]+YS );
-- or --
g.drawString( "" + (i+1), X[i] + XS[i/9], Y[i]+YS );
Listing 5.1
import java.awt.*;
import javax.swing.*;
public class PegGameSwing extends Canvas {
public static void main( String[] args ) {
new PegGameSwing();
}
public PegGameSwing() {
JFrame frame = new JFrame( "Peg Game" );
frame.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
setBackground( Color.white );
frame.getContentPane().add( this );
frame.setSize( new Dimension( WIN_WIDTH, WIN_HEIGHT ) );
frame.setVisible( true );
}
public void paint( Graphics g ) {
for (int i=0; i < 15; i++)
drawPeg( i, g );
}
private void drawPeg( int i, Graphics g ) {
g.setColor( Color.blue );
g.fillOval( X[i], Y[i], SIZE, SIZE );
g.setColor( Color.white );
g.setFont( font );
g.drawString( "" + (i+1), X[i]+XS[i/9], Y[i]+YS );
}
private static final int WIN_WIDTH = 170, WIN_HEIGHT = 172;
private static final int XPOS = 16, YPOS = 28, SIZE = 25, MARG = 5;
private static final int[] XS = { 9, 4 };
private static final int YS = 17;
private static final Font font = new Font( "Helvetica", Font.BOLD, 14 );
private static final int[] X = { 4*XPOS+MARG, // row 1
3*XPOS+MARG, 5*XPOS+MARG, // row 2
2*XPOS+MARG, 4*XPOS+MARG, 6*XPOS+MARG, // row 3
1*XPOS+MARG, 3*XPOS+MARG, 5*XPOS+MARG, 7*XPOS+MARG, // row 4
0*XPOS+MARG, 2*XPOS+MARG, 4*XPOS+MARG, 6*XPOS+MARG, 8*XPOS+MARG };
private static final int[] Y = { 0*YPOS+MARG, // row 1
1*YPOS+MARG, 1*YPOS+MARG, // row 2
2*YPOS+MARG, 2*YPOS+MARG, 2*YPOS+MARG, // row 3
3*YPOS+MARG, 3*YPOS+MARG, 3*YPOS+MARG, 3*YPOS+MARG, // row 4
4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG };
}
To receive "mouse pressed" events the MouseListener interface must be implemented. The only method that needs to be defined is mousePressed(). The X and Y pixel locations of the mouse pick are retrieved from the MouseEvent parameter. How shall we transform these two values into one integer that represents the selected peg?
If the pegs were layed out in a regular grid, then we could use integer division on the X and Y values to compute the corresponding peg. But the triangular arrangement doesn't seem to be sufficiently regular. Perhaps we could compute the correct row with integer division, and then use multiple tiers of "case" statements to figure out the correct column.
On the other had, if we are willing to throw a little extra memory at the problem, we could overlay a "fine grained" grid on the game board, and have each grid location reference a single peg. We could even let seemingly unused grid locations reference some reasonable peg. Given the mapping demonstrated below, the user can be fairly sloppy horizontally when selecting pegs 1, 2, 3, 4, 6, 7, and 10. The cells data structure in listing 5.2 implements this strategy.
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 5 5 6 6 6 6 7 7 7 8 8 9 9 10 10 10 11 11 12 12 13 13 14 14 15 15Now that we have a regular grid, we can use integer division to transpose X and Y pixel values into column and row cell values. The division operations are a little sloppy - they do not account for the MARG (margin) constant. The only discernable ill-effect is the possibility of computing a column or row that is one too high. This edge effect is handled by the if statements below. The column and row computed can then be used to look-up the correct peg.
x = x / XPOS; if (x > 9) x = 9; y = y / YPOS; if (y > 4) y = 4; int i = cells[y][x];Listing 5.2
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
public class PegGameSwing extends Canvas implements MouseListener {
private boolean[] pegsPresent = new boolean[15];
public static void main( String[] args ) {
new PegGameSwing();
}
public PegGameSwing() {
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
JFrame frame = new JFrame( "Peg Game" );
frame.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
setBackground( Color.white );
addMouseListener( this );
frame.getContentPane().add( this );
frame.setSize( new Dimension( WIN_WIDTH, WIN_HEIGHT ) );
frame.setVisible( true );
}
public void paint( Graphics g ) {
for (int i=0; i < pegsPresent.length; i++)
drawPeg( i, g );
}
public void mousePressed( MouseEvent e ) {
int x = e.getX(), y = e.getY();
x = x / XPOS; if (x > 9) x = 9;
y = y / YPOS; if (y > 4) y = 4;
int i = cells[y][x];
Graphics g = getGraphics();
pegsPresent[i] = ! pegsPresent[i];
drawPeg( i, g );
}
public void mouseEntered( MouseEvent e ) { }
public void mouseExited( MouseEvent e ) { }
public void mouseClicked( MouseEvent e ) { }
public void mouseReleased( MouseEvent e ) { }
private void drawPeg( int i, Graphics g ) {
if (pegsPresent[i]) {
g.setColor( Color.blue );
g.fillOval( X[i], Y[i], SIZE, SIZE );
g.setColor( Color.white );
} else {
g.setColor( Color.white );
g.fillOval( X[i], Y[i], SIZE, SIZE );
g.setColor( Color.blue );
}
g.setFont( font );
g.drawString( "" + (i+1), X[i]+XS[i/9], Y[i]+YS );
}
private static final int XPOS = 16, YPOS = 28, SIZE = 25, MARG = 5;
private static final int WIN_WIDTH = 170, WIN_HEIGHT = 172;
private static final int[] XS = { 9, 4 };
private static final int YS = 17;
private static final Font font = new Font( "Helvetica", Font.BOLD, 14 );
private static final int[] X = { 4*XPOS+MARG, // row 1
3*XPOS+MARG, 5*XPOS+MARG, // row 2
2*XPOS+MARG, 4*XPOS+MARG, 6*XPOS+MARG, // row 3
1*XPOS+MARG, 3*XPOS+MARG, 5*XPOS+MARG, 7*XPOS+MARG, // row 4
0*XPOS+MARG, 2*XPOS+MARG, 4*XPOS+MARG, 6*XPOS+MARG, 8*XPOS+MARG };
private static final int[] Y = { 0*YPOS+MARG, // row 1
1*YPOS+MARG, 1*YPOS+MARG, // row 2
2*YPOS+MARG, 2*YPOS+MARG, 2*YPOS+MARG, // row 3
3*YPOS+MARG, 3*YPOS+MARG, 3*YPOS+MARG, 3*YPOS+MARG, // row 4
4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG };
private static final int[][] cells = { {0,0,0,0,0,0,0,0,0,0}, // row 1
{1,1,1,1,1, 2,2,2,2,2}, // row 2
{3,3,3,3, 4,4, 5,5,5,5}, // row 3
{6,6,6, 7,7, 8,8, 9,9,9}, // row 4
{10,10, 11,11, 12,12, 13,13, 14,14} }; // row 5
}
Let's migrate the first three to a new PegGameModel class. See listing 5.3.
What interaction seems necessary from the PegGameModel object to the PegGameView object?
When attemptMove() finds a legal move, it either needs to refresh the entire user interface, or, it needs to vacate two peg locations and fill one peg location. The latter choice would be more efficient. Having the model change the state of individual peg locations in the view would seem to be a sufficient contract to decouple one from the other.
interface PegGameView {
void setPeg( int i, boolean state );
}
class PegGameModel {
private PegGameView view;
...
public void attemptMove( int from, int to ) {
...
pegsPresent[ jumpTable[i][0]-1 ] = false;
...
view.setPeg( jumpTable[i][0]-1, false);
The removePeg() method in listing 5.3 will be introduced next.Listing 5.3
class PegGameModel {
private PegGameView view;
private boolean[] pegsPresent = new boolean[15];
public PegGameModel( PegGameView v ) {
view = v;
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
}
public void removePeg( int i ) {
pegsPresent[i] = false;
}
public void attemptMove( int from, int to ) {
from++; to++;
for (int i=0; i < jumpTable.length; i++)
if (from == jumpTable[i][0] && to == jumpTable[i][1]
&& pegsPresent[ jumpTable[i][0]-1 ] // if "from" position is filled
&& pegsPresent[ jumpTable[i][2]-1 ] // if "jumped" position is filled
&& ! pegsPresent[ jumpTable[i][1]-1 ]) { // if "to" position is vacant
pegsPresent[ jumpTable[i][0]-1 ] = false; // vacate the "from" position
pegsPresent[ jumpTable[i][2]-1 ] = false; // vacate the "jumped" position
pegsPresent[ jumpTable[i][1]-1 ] = true; // fill the "to" position
view.setPeg( jumpTable[i][0]-1, false);
view.setPeg( jumpTable[i][2]-1, false);
view.setPeg( jumpTable[i][1]-1, true);
break;
} }
private int jumpTable[][] = { {1,4,2}, {1,6,3},
{2,7,4}, {2,9,5},
/* {a,b,c} */ {3,8,5}, {3,10,6},
/* a = "from" position */ {4,6,5}, {4,1,2}, {4,11,7}, {4,13,8},
/* b = "to" position */ {5,14,9}, {5,12,8},
/* c = "jumped" position */ {6,4,5}, {6,13,9}, {6,15,10}, {6,1,3},
{7,2,4}, {7,9,8},
{8,3,5}, {8,10,9},
{9,2,5}, {9,7,8},
{10,8,9}, {10,3,6},
{11,13,12}, {11,4,7},
{12,5,8}, {12,14,13},
{13,11,12}, {13,15,14}, {13,6,9}, {13,4,8},
{14,12,13}, {14,5,9},
{15,13,14}, {15,6,10} };
}
The PegGameDos class should now implement the contract that the
PegGameModel expects. It creates the model object, and initializes
that object with a reference to itself. Now that the "business logic"
attributes and methods have been removed from the view, it must ask the
model to attemptMove(). A new method was needed in the model to update
its state at the start of the game when the user designates where the
initial hole should be. Note the removePeg() call below.
public class PegGameDos implements PegGameView {
...
public PegGameDos() {
...
PegGameModel model = new PegGameModel( this );
...
System.out.print( "Select initial hole: " );
...
pegsPresent[from] = false;
model.removePeg( from );
...
while (true) {
display();
...
model.attemptMove( from, to );
} }
Listing 5.3 shows the peg state being maintained in the model, but, in
listing 5.4, it has been replicated (or cached) in the view. This
allows the view to redisplay itself independent of the model.Listing 5.4
interface PegGameView {
void setPeg( int i, boolean state );
}
public class PegGameDos implements PegGameView {
private boolean[] pegsPresent = new boolean[16];
private String blanks = " ";
public static void main( String[] args ) {
new PegGameDos();
}
public PegGameDos() {
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
PegGameModel model = new PegGameModel( this );
String input;
int from, to;
display();
System.out.print( "Select initial hole: " );
input = IOutils.getKeyboard();
if (input.equals(""))
return;
from = (int) input.charAt(0) - 'a';
pegsPresent[from] = false;
model.removePeg( from );
while (true) {
display();
System.out.print( "Move (from to): " );
input = IOutils.getKeyboard();
if (input.equals(""))
return;
from = input.charAt(0) - 'a';
to = input.charAt(2) - 'a';
model.attemptMove( from, to );
} }
public void setPeg( int i, boolean state ) { pegsPresent[i] = state; }
public void display() {
System.out.println();
for (int i=0, row=0; row < 5; row++) {
System.out.print( blanks.substring( row*3 ) );
for (int col=0; col <= row; col++, i++)
if (pegsPresent[i])
System.out.print( "<" + ((char)('A'+i)) + ">" + " " );
else
System.out.print( " " + ((char)('a'+i)) + " " );
System.out.print( "\n\n" );
} } }
Now that we have the model, the interface, and the DOS view working,
let's complete the implementation of the Swing view.How does listing 5.2 need to evolve in order to complete the PegGame Swing implementation?
Lets first set-up the roles and relationship of model and view. This is almost identical to the DOS view.
public class PegGameSwing extends Canvas implements MouseListener, PegGameView {
...
private PegGameModel model;
...
public PegGameSwing() {
...
model = new PegGameModel( this );
The current user interaction functionality is limited to selecting and
removing pegs. This needs to be extended to support jumping pegs. Is
there a way of separating select initial hole and move (from to)
selection events? How can the from and to selections be
distinguished?All user selection events are funneled through the mousePressed() method. Unless we introduce new GUI features (like JButton components, or modifier keys), well need to conceive of some way for this one method to serve three different purposes: remove a peg to start the game, select the from peg, and select the to hole.
State machine describes an application whose response to external inputs depends upon its current state. An example is a push button on/off switch for a radio. It has two states: ON, and OFF; and one input: push. When the machine is in the OFF state and receives a push input, its response is to go to the ON state. When its in the ON state and a push is received, its response is to return to the OFF state.
In our application, the only input is select. The number of responses needed is three: remove, from, and to. Each response corresponds to a state. The program starts off waiting for a remove request. This could be described as the REMOVE state. A select input causes the designated peg to be removed, and transitions the application to the FROM state. The next select input toggles the background of the selected peg, and sets the program to the TO state. One more select input completes a move request, and returns the application to the FROM state. The program cycles between the FROM and TO states until no more moves are possible.
How can the application enforce this flow of control?
An integer attribute could be used to remember the programs current state. A value of 0 could represent the REMOVE state, 1 could designate the FROM state, and 2 could map to the TO state.
When the TO hole is selected, how will we remember what the previous FROM peg was?
A second integer attribute would work. Or, we could try assigning both responsibilities to the state attribute we just specified. That attribute could hold the from peg (a value between 0 and 14) when the program transitions to the TO state. After the to hole is selected, the state attribute could be assigned some special value (-1 is used below) to represent the FROM state. Finally, a second special value could designate the initial REMOVE state (-2 is used below).
The implementation below exercises an additional slight optimization. If the user wants to unselect her from peg (firstPeg == i), there is no need to repaint() the entire board, just update that single location.
private int firstPeg = -2;
public void mousePressed( MouseEvent e ) {
...
if (firstPeg == -2) { // initial state - select initial hole
pegsPresent[i] = false;
drawPeg( i, g );
model.removePeg( i );
firstPeg = -1;
} else if (firstPeg == -1) { // select from peg
firstPeg = i;
drawPeg( i, g );
} else if (firstPeg == i) { // unselect from peg
firstPeg = -1;
drawPeg( i, g );
} else { // select to hole
model.attemptMove( firstPeg, i );
firstPeg = -1;
repaint();
} }
The final change is an update to drawPeg(). The from peg needs to be
drawn in red while the application is waiting for the to hole
selection. This can be accomplished by testing whether the specified
peg is the previously selected from peg.
private void drawPeg( int i, Graphics g ) {
...
if (i == firstPeg) g.setColor( Color.red );
else g.setColor( Color.blue );
Listing 5.5
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
public class PegGameSwing extends Canvas implements MouseListener, PegGameView {
private int firstPeg = -2;
private boolean[] pegsPresent = new boolean[15];
private PegGameModel model;
public static void main( String[] args ) {
new PegGameSwing();
}
public PegGameSwing() {
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
JFrame frame = new JFrame( "Peg Game" );
frame.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
setBackground( Color.white );
addMouseListener( this );
frame.getContentPane().add( this );
frame.setSize( new Dimension( WIN_WIDTH, WIN_HEIGHT ) );
frame.setVisible( true );
model = new PegGameModel( this );
}
public void setPeg( int i, boolean state ) {
pegsPresent[i] = state;
}
public void paint( Graphics g ) {
for (int i=0; i < pegsPresent.length; i++)
drawPeg( i, g );
}
public void mousePressed( MouseEvent e ) {
int x = e.getX(), y = e.getY();
x = x / XPOS; if (x > 9) x = 9;
y = y / YPOS; if (y > 4) y = 4;
int i = cells[y][x];
Graphics g = getGraphics();
if (firstPeg == -2) { // initial state - select starting hole
pegsPresent[i] = false;
drawPeg( i, g );
model.removePeg( i );
firstPeg = -1;
} else if (firstPeg == -1) { // select source peg
firstPeg = i;
drawPeg( i, g );
} else if (firstPeg == i) { // unselect source peg
firstPeg = -1;
drawPeg( i, g );
} else { // select destination hole
model.attemptMove( firstPeg, i );
firstPeg = -1;
repaint();
} }
public void mouseEntered( MouseEvent e ) { }
public void mouseExited( MouseEvent e ) { }
public void mouseClicked( MouseEvent e ) { }
public void mouseReleased( MouseEvent e ) { }
private void drawPeg( int i, Graphics g ) {
if (pegsPresent[i]) {
if (i == firstPeg) g.setColor( Color.red );
else g.setColor( Color.blue );
g.fillOval( X[i], Y[i], SIZE, SIZE );
g.setColor( Color.white );
} else {
g.setColor( Color.white );
g.fillOval( X[i], Y[i], SIZE, SIZE );
g.setColor( Color.blue );
}
g.setFont( font );
g.drawString( "" + (i+1), X[i]+XS[i/9], Y[i]+YS );
}
private static final int XPOS = 16, YPOS = 28, SIZE = 25, MARG = 5;
private static final int WIN_WIDTH = 170, WIN_HEIGHT = 172;
private static final int[] XS = { 9, 4 };
private static final int YS = 17;
private static final Font font = new Font( "Helvetica", Font.BOLD, 14 );
private static final int[] X = { 4*XPOS+MARG, // row 1
3*XPOS+MARG, 5*XPOS+MARG, // row 2
2*XPOS+MARG, 4*XPOS+MARG, 6*XPOS+MARG, // row 3
1*XPOS+MARG, 3*XPOS+MARG, 5*XPOS+MARG, 7*XPOS+MARG, // row 4
0*XPOS+MARG, 2*XPOS+MARG, 4*XPOS+MARG, 6*XPOS+MARG, 8*XPOS+MARG };
private static final int[] Y = { 0*YPOS+MARG, // row 1
1*YPOS+MARG, 1*YPOS+MARG, // row 2
2*YPOS+MARG, 2*YPOS+MARG, 2*YPOS+MARG, // row 3
3*YPOS+MARG, 3*YPOS+MARG, 3*YPOS+MARG, 3*YPOS+MARG, // row 4
4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG, 4*YPOS+MARG };
private static final int[][] cells = { {0,0,0,0,0,0,0,0,0,0}, // row 1
{1,1,1,1,1, 2,2,2,2,2}, // row 2
{3,3,3,3, 4,4, 5,5,5,5}, // row 3
{6,6,6, 7,7, 8,8, 9,9,9}, // row 4
{10,10, 11,11, 12,12, 13,13, 14,14} }; // row 5
}