15 Square Puzzle

The puzzle consists of a 4 by 4 grid containing 15 slideable squares and one blank space. The puzzle is initialized by randomly sliding the squares until they are sufficiently "shuffled". The player then moves individual squares, or entire rows/columns until the pieces are back in ascending order.

To make moves, specifying the "to" and "from" positions would be burdensome. Instead, moves are identified by specifying a square that is in the same row or column as the blank space. The application then responds by moving all squares between the blank space and the designated square in the direction of the blank space.

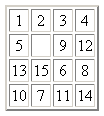
The project

Write an implementation that supports the demonstrated DOS user interface. Later, modify the application to support a user-specified width and height. Finally, adapt the design to include a graphical user interface like that to the right.

Five iterations:

  1. Display a 4x4 grid, receive input, update display
  2. Randomize the squares
  3. Implement single-square move
  4. Implement multi-square move
  5. Refactor to support user-defined width and height

Iteration 1

What data structure would best support the functionality we are trying to capture. With the DOS user interface, we need to model rows and columns. With the subsequent graphical user interface, rows and columns will be managed for us by the GridLayout component. A one-dimensional array optimizes simplicity, but requires the developer to row-column logic. A two-dimensional array optimizes row-column logic, but requires a double loop construct every time any element is accessed.

   

> java FifteenPuzzleDos

 9  3  4 12
10 13  5  8
    2 14  1
 7  6 11 15

Move: 9

    3  4 12
 9 13  5  8
10  2 14  1
 7  6 11 15

Move: 12

 3  4 12
 9 13  5  8
10  2 14  1
 7  6 11 15
In the spirit of "make it run", the first iteration will be limited to the subset of functionality demonstrated to the right. When the user specifies a "move", the program should find the corresponding square, add 10 to that square's value, and re-display the puzzle.

Instructions and issues:

  • Decide on the data structure(s) to model slideable squares and stationary positions.
  • Create a FifteenPuzzleDos class that can encapsulate all the state and behavior necessary to present the illusion that a FifteenPuzzle object truly exists.
  • Specify display()and move() behaviors for your class.
  • All the business logic for the puzzle has been captured in the FifteenPuzzleDos class. What remains to be written is the code that choreographs the users desires and the classs services. Create an instance of the FifteenPuzzleDos class in main(), and use the following code to drive the user interaction. 
    int number;
while (true) {
  System.out.print( "\nMove: " );
  number = Integer.parseInt( IOutils.getKeyboard() );
  if (number == 0)
    break;
}

Iteration 2

The puzzle is begun once the squares have been sufficiently scrambled. How is that done in the real game? Do you take all the squares out of the board, and then put them back on the board in jumbled order? I hope not. When I first implemented this puzzle, I wrote a very simple algorithm that basically did just that. It wasnt until the next day that I realized you can make the puzzle unsolvable by truly randomizing the squares.

   
> java FifteenPuzzleDos

 1  2  3  4
 5  6  7  8
 9 10 11 12
13 14 15

Move: 3

 1  2 13  4
 5  6  7  8
 9 10 11 12
13 14 15

Move: 13

 1  2 23  4
 5  6  7  8
 9 10 11 12
13 14 15

Move: 13

 1  2 23  4
 5  6  7  8
 9 10 11 12
23 14 15
In real life, you scramble the squares by randomly pushing them around. In this iteration, scramble the numbers associated with the square positions before the board is displayed the first time. Instructions and issues:

Iteration 3

Let's add legitimate "move" functionality in this iteration. Any square that is adjacent to the blank space can be swapped with the blank by specifying its number. If the square is not adjacent, nothing happens. Instructions and issues:

Iteration 4

Instead of having to move each square individually; it would be nice to be able to move two or more squares in the same row or column at the same time. Instructions and issues:

Iteration 5

The more general problem is often easier to solve, and in programming, the more general design may be easier to implement, may operate faster on the machine, and can actually be better understood by the user. In addition, it will almost certainly be easier to maintain, for often we won't have to change anything at all to meet changing circumstances that fall within its range of generality. [Gerald Weinberg]
This would have been invaluable advice before we started the first iteration. A 4-by-4 grid is certainly the most common implementation of this puzzle, but there is nothing inherently sacred about that configuration. Let's use this iteration to test the Weinberg assertion. Refactor the current implementation to request the dimensions of the puzzle's grid. Instructions and issues:

Iteration 1 - implementation

Since we need to model sixteen stationary positions and fifteen slideable squares, does that require two different data structures? Lets think about what an array represents. It is a sequential list of homogeneous variables. And a variable is an address (or memory location) that holds a value. Each position in our puzzle is always hosting a square (or the one non-square). So, a puzzle position corresponds to a variable, and the square that is currently hosted by a position corresponds to the value assigned to that variable. Since there is more than one position, using an array to maintain the position-square state would offer significant leverage.

The next decision to face is what kind of array? One-dimensional, or two-dimensional? The latter would seem to be an obviously natural mapping. But, whenever the array needs to be initialized or searched, a double loop construct is necessary. Because a a single loop is half as much effort as a double loop, a one-dimensional array was chosen in listing 2.1.

Using a one-dimensional array means that we will have to do for ourselves what the compiler is happy to do for us make a one-dimensional address space appear as though it is actually two-dimensional. The logic "squares[i * 4 + j]" in the display() function is where the 1D-to-2D magic happens. If we had chosen a 2D data structure, the code would have been reduced to "squares[i][j]".

Listing 2.1 uses a constructor to load the values 1-15 into positions 0-14.

A value of zero was chosen to model the blank space. The actual "blank" is produced with logic encapsulated in the format() function.

The move() function doesnt require any more sophistication than sequential search.

Once the FifteenPuzzleDos class exists, main() is easy: create an instance of this remarkable tool, and iteratively display the board, solicit moves, and execute each move.

Listing 2.1

Iteration 2 - implementation

To scramble the board, we could iteratively find random squares that are adjacent to the blank space, and swap them with the blank. Or, we could imagine that the blank is the active agent. Perhaps it is like a worm wandering aimlessly throughout the board, scrambling squares in its wake.

Since the board needs to start out in a random state, the constructor should be assigned this initialization responsibility.

In the previous iteration, the blank started at position 15. From here, it can choose to travel to either of its neighbors positions 14 or 11. If it chose position 11, its next array of choices would be: 7, 10, or 15. It would seem useful to have a tool capable of computing all the neighbors of a specified square. Lets discuss the contract - what is required by, and what is expected of - for a find neighbors function.

It needs to know the position for which the neighbors are being requested. It then needs to return a list of the legal neighbors. Is the number of neighbors always the same? Some positions have four neighbors, but others have two or three. So, the function needs to return two things: the list of neighbors, and the number of elements in that list. We could try to mash both of these items into the functions return value. This would work if we returned the list of neighbors, and, established the convention that the first element in the list is the number of neighbors in the list.

Another choice would be to return a smart array an array that knows its own size. Arrays in Java provide that capability if they are created to be the correct size. Using this option would require creating a new array object each time our new findNeighbors function is called.

Yet another choice would use an output array parameter for the list of neighbors, and the return value of the function for the number of neighbors that were written to the array parameter. The user of the findNeighbors function passes in an array of length four, and the function populates the array with two, three, or four elements. This is the choice made in listing 2.2.

Once we have a findNeighbors abstraction (the implementation of which is conveniently deferred for now), the rest is easy. Simply pick a random element in the neighbors array, swap that square with the blank, and update the value of the blank variable. To pick a random element, we use the same nextInt() method as was used in the Mastermind project. That means a Random object will need to be added to our classs suite of attributes.

Listing 2.2 moves the blank 200 times in the scramble() method. This seems to produce a sufficiently random starting position.

The final piece is the findNeighbors() method. If the blank is on the top row, there is no neighbor above the blank. If the blank is on the bottom row, left column, or right column, then there is no neighbor: below, left, or right, respectively. Once the boundary conditions have been satisfied, we can populate the neigborsArray.

The above neighbor for position 4 is 0. The above neighbor for position 8 is 4. Do we have to write code to manually capture the above neighbor for all 12 positions that have an above neighbor? Or can we compute that neighbor in some general fashion?

Fortunately, there is a pattern every above neighbor can be found by subtracting 4 from the position of the original square. A similar computation works for finding below, left, and right neighbors. Listing 2.2 collects the complete changes for this iteration.

Listing 2.2

Iteration 3 - implementation

The logic for finding and processing the blank space was implemented in four methods: tryAbove(), tryBelow(), tryLeft(), and tryRight(). This could have been collapsed into a single function with some resourceful data structures. The choice of four separate functions was made in anticipation of the "move an entire row or column" functionality introduced in the next iteration.

Each function has the same form. If the specified position is "on the edge", then do nothing. If the blank space is not found, then do nothing. Otherwise, swap the specified position and its neighbor. If this function succeeded, then there is no need to evaluate the other functions.

Notice the logic for evaluating boundary conditions and direction. The modulus operator (aka [also known as] - the "remainder" operator) is very nondescript, but the leverage it offers is invaluable in many contexts. Here, it is perfect for identifying if the specified position is on the left or right edge. Many of the values hard-wired here will need to be fixed in iteration 4 when the width and height of the puzzle are configurable by the user. The modulus operator is a remarkable tool in the hands of a craftsman.

Listing 2.3

Iteration 4 - implementation

The only change necessary is to extend the conditional expression "squares[pos-4] != 0" to include an additional test. A loop construct could have been crafted to propagate the move request until the blank space is encountered. But, recursion is the perfect tool when a function needs to feel its way along until a desired end state is found. When that state is reached, the preceding path to that state can be easily retraced by simply hanging on as the compiler unrolls the function call stack. Please see appendix C for additional coverage of recursion.

Notice that each tryXxx() function calls itself until the edge is found. If the neighbor is the blank - or - a downstream neighbor is a neighbor to the blank, then the current square should be swapped, and all upstream neighbors should be told to swap themselves.

Listing 2.4

Iteration 5 - implementation

The transformation is remarkably painless. The width is substituted in many obvious places. The height and width are used to bound the loops in display(). The only non-trivial change is - This is simply computing the threshold of square positions that fall on the bottom row.

Never solve a specific problem, when the solution to a general problem (that can be reasonably anticipated) is no more expensive.

Listing 2.5