 In Mastermind, player one selects a sequence of four colored pegs, and
player two makes guesses until she has identified the sequence. There
are six colors, and each color may be used more than once. As guesses
are made, the feedback provided is: a black peg for each correct color
in the correct position, and a white peg for each correct color in the
wrong position.
In Mastermind, player one selects a sequence of four colored pegs, and
player two makes guesses until she has identified the sequence. There
are six colors, and each color may be used more than once. As guesses
are made, the feedback provided is: a black peg for each correct color
in the correct position, and a white peg for each correct color in the
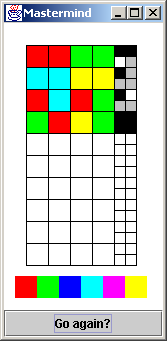
wrong position.In the example to the right, the program is playing the role of player one. The user of the program made an initial guess of: red, red, green, green. The program evaluated the guess, and returned two black pegs, and one white peg. The second guess was: cyan, cyan, yellow, yellow. The response returned by the program was one black peg.
The feedback from the first guess indicates that the answer contains: two reds and one green, or two greens and one red. From the second guess we know there is exactly one cyan, or one yellow. The two guesses taken together account for all four pegs, so we know there are no blue or magenta pegs.
For the third guess, lets assume there are two reds and one green (from the feedback for the first guess), and one cyan (from the feedback for the second guess). The order we put these colors in should not violate what we know to be true from previous responses. The order chosen for the third guess was: red, cyan, red, green. The evaluation returned one black peg and one white peg.
Since the overlap from the first guesss two possible scenarios is one red and one green, the response in the third guess is telling us: there is one red and one green, there is no cyan, and we made the wrong choice with respect to both the first and second responses. We should have chosen: two greens, one red, and one yellow.
Now that we have identified the colors, we need to work on the order. Every guess needs to be consistent with the feedback from all previous guesses. The ordering (red, green, green, yellow) would have been a valid guess. Instead, the user randomly chose (green, red, yellow, green) and won the game.
> java MastermindDos
Input: 5 5 4 4
0 0
Input: 3 3 2 2
0 2
Input: 1 2 3 1
2 1
Input: 1 2 0 3
2 0
Input: 1 1 3 3
4 0
The program should also return the answer when the user enters the character ‘a’.
> java MastermindDos
Input: a
0 4 1 0
Input: 4 0 1 0
2 2
Input: 0 4 1 0
4 0
The project is divided into three iterations:
To this end, start the project by implementing the user interaction functionality. The program needs to: prompt for input, receive input, evaluate the input, supply a default answer, and exit.
More computing sins are committed in the name of efficiency than for any other single reason - including blind stupidity. [William Wulf] Improved efficiency comes at the cost of practically every other desirable software property. [Martin Carroll and Margaret Ellis]
> java MastermindDos
Input: 1 2 3 4
3 7
Input: 2 3 4 5
5 9
Input: a
0 0 0 0
Input: x
>
Instead of dealing with Java's standard input functionality, let's use the following utility.
import java.io.*;
public class IOutils {
public static String getKeyboard() {
BufferedReader in = new BufferedReader(
new InputStreamReader( System.in ));
String str = null;
try {
str = in.readLine();
} catch ( IOException ex ) { ex.printStackTrace(); }
return str;
} }
Instructions and issues:
It has been said, "Abstraction is the discipline of creating useful fictions." In this project, it would be nice if we could hide (or delegate): the generation of the random sequence, and evaluating all user guesses. The former is state, and the latter is behavior. A class is the object-oriented mechanism by which we encapsulate or "co-locate" state and behavior.
This class will incorporate the core "business logic" of the game. A common label for this type of component is "model". The functionality that will remain in main() will be "user interface" in its orientation. Dividing responsibilities along these lines will allow us in a later chapter to replace the DOS command line user interface with a graphical user interface. At that point, we should be able replace one "look and feel" with another, without having to disturb our "model" component at all.
Encapsulation case study In 1989, a formula was published for calculating the optimal flight path for an aircraft on final approach. A printing error resulted in an '8' being transposed to a '6'. As the effect of this was minor, the mistake was not picked up for some time. It was only discovered after a number of complaints from maintenance crews about the level of maintenance required due to hard landings.
Three different projects had used the bad formula in developing software segments of landing control systems. Two groups used C++ and object technology, the third used C and structured methods. When it became clear that there was an error in the distributed version of the formula, all three groups were informed and instructed by the authorities to fix their code.
The first group had not used formal class library control approaches. It took them 5 weeks to find every instance of the formula in their code, correct it, and then recompile. The C group had embedded the formula in a set of library functions. They only needed to rework the library functions, recompile, build, and test - about 4 days. The third group had placed the formula inside a set of specially contructed classes that were made available through a class library. They were able to update the formula, recompile only the affected components, build, and test - 1.5 days total.
[Ian Graham, "Reuse: A Key to Successful Migration", Object Magazine, October 1995, p83]
The goal of this iteration is to support this slightly modified main() and the following output.
class MastermindDos {
public static void main( String[] args ) {
MastermindModel mm = new MastermindModel();
int[] input = new int[4], blackWhite = new int[2], answer;
while (blackWhite[0] != input.length) {
System.out.print( "Input: " );
String str = IOutils.getKeyboard();
System.out.print( " " );
if (str.charAt(0) == 'a') {
answer = mm.getAnswer();
System.out.println( answer[0] +" "+ answer[1] +' '+ answer[2]
+' '+ answer[3] );
continue;
}
if ( ! parse( str, input )) {
System.out.println( "invalid input" );
continue;
}
mm.guess( input, blackWhite );
System.out.println( blackWhite[0] + " " + blackWhite[1] );
} } }
// Input: a
// 0 4 1 0
// Input: 4 0 1 0
// 2 0
// Input: 0 4 0 1
// 2 0
Instructions and issues:
It is not uncommon to find looping code written with input logic replicated before the loop and at the bottom of the loop. The purpose is to allow the loop construct (the for or while statement) to test the initial input, and all subsequent input. This is happening in listing 2.1. For discussion purposes, here is a parallel example.
System.out.print( "Input: " );
String str = IOutils.getKeyboard();
while ( ! str.equals("x")) {
System.out.println( " " + str );
System.out.print( "Input: " );
str = IOutils.getKeyboard();
}
// Input: the first line of input
// the first line of input
// Input: a second line
// a second line
// Input: x
Replicated code is always a maintenance liability. The only constant
in life is change. When the prompt and input functionality requires
updating, it will inevitably be changed in fewer places than actually
exist. Replication of code should be vigorously avoided. We could
choose to combine the input statement and the boolean expression of the
while loop. This would seemingly demonstrate our mastery of the
language - the return value of an assignment expression is the value
received by the left-hand operand. But, it could be well-argued that
this is "write only" code - any attempt to subsequently read this code
will be an all too viscous experience. Additionally, the prompt
functionality continues to be replicated.
String str;
System.out.print( "Input: " );
while ( ! (str = IOutils.getKeyboard()).equals("x")) {
System.out.println( " " + str );
System.out.print( "Input: " );
}
String str;
while (true) {
System.out.print( "Input: " );
str = IOutils.getKeyboard();
if (str.equals("x"))
break;
System.out.println( " " + str );
}
Multiple levels of scopeTwo common programming conventions are: code should read from top to bottom; and single entry, single exit. Both of these idioms are used to prohibit use of the goto statement. The second one is also used to discourage use of multiple return statements in a function, and the break and continue statements in a loop. The parse() function of listing 2.1 follows both conventions.
public static boolean parse( String str, int[] outParameter ) {
boolean returnValue = true;
StringTokenizer st = new StringTokenizer( str );
if (st.countTokens() != 4)
returnValue = false;
else {
int i = 0;
while (st.hasMoreTokens() && returnValue != false) {
The parse() function in listing 2.2 does not follow the letter of the
"single entry, single exit" law, but it does follow the spirit to
promote code readability. The code above (from listing 2.1), adds an
extra level of scope and indentation. This effectively adds one more
ball to the reader's juggling challenge.It is commonly accepted that humans are only capable of juggling seven simultaneous tasks, concerns, and distractions. The code below (from listing 2.2) removes one of those "balls" by eliminating the need for the else clause, and the compound expression in the while statement, by employing multiple return statements.
public static boolean parse( String str, int[] outParameter ) {
StringTokenizer st = new StringTokenizer( str );
if (st.countTokens() != 4)
return false;
int i = 0;
while (st.hasMoreTokens()) {
There is also a substantive difference in the logic of the two main()
functions. Listing 2.1 uses else clauses, while listing 2.2 uses break
and continue statements. The reader can decide which version is easier
to read.Return value versus out parameter
Notice the evaluate() function in listing 2.1. Functions should prefer to return results through their return value, rather than through output parameters. But in this implementation, every time the function is called, a new integer array object is created. While many Java programmers take great comfort in knowing that all objects are effectively free (memory is virtual and garbage collection is automatic); untoward proliferation of objects will always present a scalability issue.
public static int[] evaluate( int[] inParameter ) {
int[] outReturn = new int[2];
outReturn[0] = inParameter [0] + inParameter [1];
outReturn[1] = inParameter [2] + inParameter [3];
return output;
}
The implementation in listing 2.2 reuses a single object that is
supplied by the functions client as a parameter.
public static void evaluate( int[] inParameter, int[] outParameter ) {
outParameter[0] = inParameter[0] + inParameter[1];
outParameter[1] = inParameter[2] + inParameter[3];
}
It is a fact that the Java langauge supports a single parameter passing
mode pass by value. It is reality that when an object reference is
passed by value, the object to which that reference refers is
effectively passed by reference. The object reference copied to the
stack when a function is invoked is effectively a pointer. When the
object reference is de-referenced in the body of the function, the
state of the original object can, and will, be changed. Since arrays
are implemented as objects in Java, the outParameter argument in
listing 2.2 is an in/out parameter. See Appendix A for an additional
discussion of parameter passing in Java.Listing 2.1 - original implementation
import java.util.StringTokenizer;
class MastermindDos {
public static boolean parse( String str, int[] outParameter ) {
boolean returnValue = true;
StringTokenizer st = new StringTokenizer( str );
if (st.countTokens() != 4)
returnValue = false;
else {
int i = 0;
while (st.hasMoreTokens() && returnValue != false) {
try {
outParameter[i] = Integer.parseInt( st.nextToken() );
} catch (NumberFormatException ex) {
returnValue = false;
}
if (outParameter[i] < 0 || outParameter[i] > 5)
returnValue = false;
i += 1;
} }
return returnValue;
}
public static int[] evaluate( int[] input ) {
int[] output = new int[2];
output[0] = input[0] + input[1];
output[1] = input[2] + input[3];
return output;
}
public static void main( String[] args ) {
int[] input = new int[4];
int[] output;
System.out.print( "Input: " );
String str = IOutils.getKeyboard();
while ( ! str.equals("x")) {
System.out.print( " " );
if (str.charAt(0) == 'a') {
System.out.println( "0 0 0 0" );
} else if ( ! parse( str, input )) {
System.out.println( "invalid input" );
} else {
output = evaluate( input );
System.out.println( output[0] + " " + output[1] );
}
System.out.print( "Input: " );
str = IOutils.getKeyboard();
} } }
Listing 2.2 - refactored implementation
import java.util.StringTokenizer;
class MastermindDos {
public static boolean parse( String str, int[] outParameter ) {
StringTokenizer st = new StringTokenizer( str );
if (st.countTokens() != 4)
return false;
int i = 0;
while (st.hasMoreTokens()) {
try {
outParameter[i] = Integer.parseInt( st.nextToken() );
} catch (NumberFormatException ex) {
return false;
}
if (outParameter[i] < 0 || outParameter[i] > 5)
return false;
i += 1;
}
return true;
}
public static void evaluate( int[] inParameter, int[] outParameter ) {
outParameter[0] = inParameter[0] + inParameter[1];
outParameter[1] = inParameter[2] + inParameter[3];
}
public static void main( String[] args ) {
int[] input = new int[4];
int[] output = new int[2];
while (true) {
System.out.print( "Input: " );
String str = IOutils.getKeyboard();
System.out.print( " " );
if (str.charAt(0) == 'x')
break;
if (str.charAt(0) == 'a') {
System.out.println( "0 0 0 0" );
continue;
}
if ( ! parse( str, input )) {
System.out.println( "invalid input" );
continue;
}
evaluate( input, output );
System.out.println( output[0] + " " + output[1] );
} } }
Should the parse() function specified in the iterations set-up be included in this abstraction? Since it is totally independent of the state maintained by the MastermindModel, lets not couple it to that class. Instead, it can exist as a stand-alone utility function.
Mastermind, as we know it today, consists of four positions and six colors. But in the future, its requirements will most certainly creep. Anticipating this fact of life now, will save time and heartache later. By introducing symbolic constants as a buffer against this kind of inevitability, we should protect our code from becoming brittle, and contracting "hardening of the software arteries." In listing 2.3, the values that would otherwise appear as hard-wired constants in the code, have been captured and hidden behind the names: NUMBER_OF_POSITIONS, and MAXIMUM_VALUE.
Notice the use of the Java standard library to generate random values in the constructor of listing 2.3. It would have been possible to use the static method random() in the class java.lang.Math. But the java.util.Random class provides a much simpler interface. Finding the right component for the problem at hand is always a challenge.
How does a person find something that is not known to exist? How does a person look up the spelling for a word in the dictionary, when you practically have to know how to spell the word before you can look it up? This dilemma of reuse has been captured in Thomas Keffer's two rules of reuse.
Computing the "black" response to a user guess is very straight-forward. Each element in the input array is compared to its counterpart in the answer array.
Listing 2.3
import java.util.Random;
public class MastermindModel {
public static final int NUMBER_OF_POSITIONS = 4;
public static final int MAXIMUM_VALUE = 5;
private Random rn = new Random();
private int[] answer = new int[NUMBER_OF_POSITIONS];
public MastermindModel() {
for (int i=0; i < answer.length; i++)
answer[i] = rn.nextInt( MAXIMUM_VALUE+1 );
}
public void guess( int[] input, int[] bw ) {
bw[0] = bw[1] = 0;
for (int i=0; i < answer.length; i++)
if (input[i] == answer[i])
bw[0]++;
}
public int[] getAnswer() {
return answer;
} }
boolean[] inputPositionsMatched = new boolean[input.length]; boolean[] answerPositionsMatched = new boolean[input.length];The next natural thing to tackle is probably computing the black count, since it takes precedence over the white count (i.e. pegs in the guess should first be used to increment the black count before they are considered in computing the white count). As black matches are found, the new housekeeping arrays are updated. See the top of the guess() method in listing 2.4.
Now that the black count is complete, and all the contributing pegs in the input and answer have effectively been set aside, let's tackle the white count. We could decide to set up a loop within a loop. The outer loop will traverse the input array, and the inner loop will traverse the answer array. Being careful to skip elements that have previously been matched, whenever a new match is found: the count is incremented, the housekeeping array is updated, and the next iteration of the outer loop is begun. See the comments in listing 2.4 for additional discussion.
Listing 2.4 - original implementation
public void guess( int[] input, int[] bw ) {
boolean[] inputPositionsMatched = new boolean[input.length];
boolean[] answerPositionsMatched = new boolean[input.length];
bw[0] = bw[1] = 0;
// Compute the black response
for (int i=0; i < input.length; i++)
if (input[i] == answer[i]) {
bw[0]++;
inputPositionsMatched[i] = true;
answerPositionsMatched[i] = true;
}
// Compute the white response
for (int i=0; i < input.length; i++) {
// If this slot in the guess has already been matched in the black loop
// then skip it here in the white loop
if (inputPositionsMatched[i])
// Go to the next iteration of the outer loop
continue;
for (int j=0; j < answer.length; j++)
// Make sure this slot in the answer has not already been matched in the
// black loop
if (!answerPositionsMatched[j] && input[i] == answer[j]) {
bw[1]++;
// We will continue to iterate through the answer array as subsequent input
// elements are evaluated, so the matched answer array needs to be updated
// but the matched input array does not
answerPositionsMatched[j] = true;
// Break out of the inner loop and return to the outer loop
break;
}
} }
I wonder if the expression, "Not being able to see the forest for the
trees," applies here. We took a very deliberate, step-by-step approach
to this programming problem. Is it possible that a different, and
perhaps better, solution would have resulted from a less deliberate,
more reflective approach? Let's consider an entirely unrelated puzzle
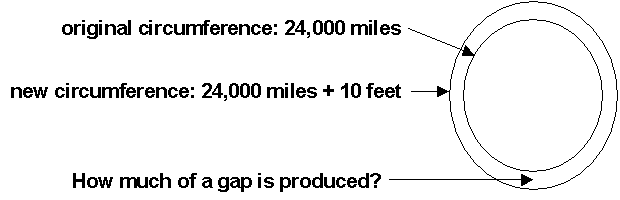
that illustrates two very different approaches.Suppose we wrap the earth with a metal band around its equator. Then we break the metal band and add 10 feet to the original circumference. If the slack that is introduced is evenly distributed around the entire equator, how much slack would there be? Enough for an amoeba, a worm, a snake, or an alligator to slither through?

A deliberate, step-by-step approach might involve a little geometry, a few facts, and a calculator.
circumference = 2 * π * radius original circumference = 24000 miles = 126720000 feet 126720000 = 2 * 3.14159 * original radius original radius = 126720000 / 6.28318 = 20168131.42 feet new circumference = 126720000 + 10 feet = 126720010 feet new radius = 126720010 / 6.28318 = 20168133.02 feet amount of slack = newRadius - originalRadius = 20168133.02 - 20168131.42 = 1.6 feetThat value seems outrageously large! How perfectly unintuitive! Simply adding 10 feet to the circumference, adds over a foot and a half of slack all the way around the equator.
Suppose now that you did not have a calculator, and your threshold of pain for doing arithmetic by hand is too low to attempt this puzzle. Is there some other approach possible?
Let's try to characterize the problem with two simultaneous equations, and then use algebra to solve for the answer.
before: C = 2πR after (X is the slack introduced): C + 10 = 2π(R + X) distributing 2π over (R + X): C + 10 = 2πR + 2πX substituting 2πR for C (because C = 2πR): 2πR + 10 = 2πR + 2πX removing the 2πR identity: 10 = 2πX solving for x: X = 10 / 2π = 5 / 3.14159 = 1.6 feetWe've achieved the same result by pushing around some abstract expressions instead of some concrete (and tedious) numbers. But, let's back up to the "X = 5 / π" equation. What happened to the problem's radius?
It's gone! It's irrelevant! The answer is the same whether the sphere employed is the earth, or a basketball.
I would characterize the first approach as exercising brute force, or, focusing on the trees; and the second approach as exercising insight, or, focusing on the forest. The first approach gave us exactly what was asked for - a single answer. The second approach presented us with a surprising epiphany. The first approach required fairly linear effort. In the second approach, the effort was fairly front-end loaded, but the subsequent solution proceeded very rapidly.
Perhaps the first approach is similar to what currently happens in large-scale software development, "Say what you do, and then do what you say." Define a process, and then use the process to mechanically solve your problems in a connect-the-dots, plug-and-chug mindset. This approach facilitates the management of large projects that need to have dozens of developers working in parallel. It makes the command and control more of a science, and less of an art. Unfortunately, it also tends to sterilize the creative process, and short-circuit the "craft-like" quality of software construction. It is fairly hostile to serendipidy and innovation.
The second approach to this geometry puzzle could be characterized as: invest in reflection until transforming insight is gleaned. That style is highly non-linear (i.e. un-manageable). It could well be described as "walking by faith." It requires an unquantifiable amount of wandering in the wilderness. But when the epiphany is received, then the promised land comes quickly. It can be nutured by an organization, but it almost always defies any attempt at being mandated or taught.
Perhaps the appropriate advice for choosing between these two approaches is, "Count the cost." If the primary criteria is manageable, then process should be emphasized. But if the primary criteria is remarkable, then reflection should be afforded the upper hand.
Don't let the urgency of the trees seduce you into neglecting the leverage of the forest.
Let's return to the algorithm for computing the white response. Is there a less direct, but more elegant approach to this problem? In the previous approach, we assumed that computing the black response first was necessary because the black computation takes precedence over the white computation. What if we computed the white response first? Would the algorithm become easier, and could we then reconcile any resulting conflict or overlap?
Let's consider the following equation about the black and white counts
number of correct colors in the correct position
+ number of correct colors in the wrong position
--------------------------------------------------
total number of correct colors
This could be refactored to the form -
correct colors in the wrong position = total - correct colors in the correct position
OR
white = total - black
Given this perspective, we see that the white count can be derived if
we can first compute the total count. Lets consider an answer of 1112
and a guess of 3311. The total count is 2 the first 1 in the guess is
totally correct, and the second 1 is partially correct. If the answer
sequence were 1234 and the guess sequence were 1155, the total count
would be 1.It appears as though the total can be computed by taking the minimum of: the number of 1s in the answer, and the number of 1s in the guess. More generally, the total is the summation of the minimums of the number of occurrences of the digits 0 through 5 in the answer and in the guess. This is modeled in the following table.
Answer is 1123 Guess is 4221 Minimum is Total is 2
Number of 0s 0 0s 0 0
1s 2 1s 1 1
2s 1 2s 2 1
3s 1 3s 0 0
4s 0 4s 1 0
5s 0 5s 0 0
Using our previous correct-color-in-the-correct-position algorithm, the
black count is 1. The white count can then be derived by subtracting 1
from 2.Is this new insight a step forward? Is it easy to count the number of occurrences of the digits 0 through 5 in both the answer and the guess? Listing 2.5 is one possible implementation. The housekeeping data structures inputPositionsMatched and answerPositionsMatched have been replaced with answerSums and inputSums. The former is initialized in the constructor, and the latter is initialized in the guess() method.
Listing 2.5 - refactored implementation
private int answer[] = new int[NUMBER_OF_POSITIONS];
private int answerSums[] = new int[MAXIMUM_VALUE+1];
public MastermindModel() {
for (int i=0; i < answer.length; i++)
answer[i] = rn.nextInt( answerSums.length );
// Initialize the answer housekeeping array
for (int i=0; i < answer.length; i++)
answerSums[ answer[i] ]++;
}
public void guess( int[] input, int[] bw ) {
bw[0] = bw[1] = 0;
// Initialize the input housekeeping array
int[] inputSums = new int[answerSums.length];
for (int i=0; i < answer.length; i++)
inputSums[ input[i] ]++;
// Compute the total
for (int i=0; i < answerSums.length; i++)
bw[1] += (inputSums[i] < answerSums[i]) ? inputSums[i] : answerSums[i];
// Compute the black response
for (int i=0; i < answer.length; i++)
if (input[i] == answer[i])
bw[0]++;
// Now, derive the white response
bw[1] = bw[1] - bw[0];
}
This new algorithm has considerably less control logic. The previous
algorithm had boundary conditions and dependencies between loops that
are not present in the new algorithm. Just like the equator geometry
puzzle, where the arithmetic approach generated the answer, but the
algebraic approach unveiled remarkable insight; I believe the first
guess() implementation met the requirements, while the second
implementation demonstrated insight and elegance.How does one develop insight? Is it nature, or nurture? Does it require left-brain, or right-brain thinking? I think it is a combination of many factors: perspiration, resourcefulness, a low threshold of pain, and a diverse background.
Perspiration. "Genius is one percent inspiration, and ninety-nine percent perspiration." [Thomas Edison] The harder we practice, the luckier we get. [football coach]
Resourcefulness. Intelligent is often used to describe people who have mastered thinking inside the box. I associate resourcefulness with thinking outside the box. Resourceful people see what everyone else has seen, and think what no one else have thought.
A low threshold of pain. I think this is the primary differentiator for inventors. Most people don't recognize, or are not sufficiently moved by, the pain they are subject to on a daily basis. Inventors are acutely intolerant of pain, and are totally consumed until it has been relieved. Software developers need to examine large, cumbersome blocks of code, and not be at peace until a simpler, higher fidelity design is discovered.
A diverse background. At an organizational level, investing in a "multi-disciplinary" approach has proven very successful. The equivalent for a person is a diverse background. The more varied a persons background, the broader their perspective, or point of view. The more perspectives an individual can bring to bear on a problem, the more likely that insight will blossom.