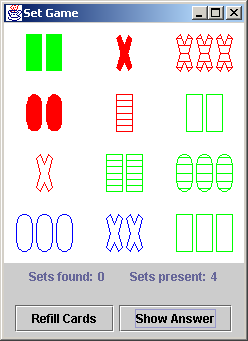
Set Puzzle

Example sets:
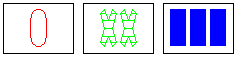	a SET same: [none] different: number, color, shape, fill
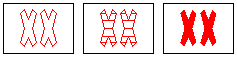	a SET same: number, color, shape different: fill
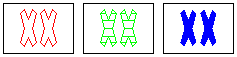	a SET same: number, shape different: color, fill
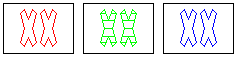	NOT a set same: number, shape different: color wrong: fill
To make it a set, one of the open fills needs to be solid, or the striped fill needs to be open.
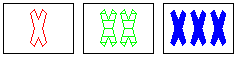	a SET same: shape different: color, number, fill
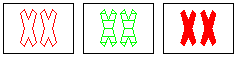	NOT a set same: shape, number different: fill wrong: color
To make it a set, one of the red colors needs to be blue, or the green color needs to be red.

public static void compute_components( int card, int[] components ) {
  components[0] = card % 3;
  components[1] = card % 9 / 3;
  components[2] = card % 27 / 9;
  components[3] = card / 27;
}

card1   0	0	1	1	2	2	0	0	1	2
card2   0	1	1	2	2	0	1	0	1	2
card3   1	1	2	2	0	0	2	0	1	2
set?	no	no	no	no	no	no	yes	yes	yes	yes

Here is an implementation ...

boolean is_a_set( int[] selected_cards ) {
   int[][] cards_and_components = new int[3][4];
   for (int i=0; i < 3; i++)
      compute_components( selected_cards[i], cards_and_components[i] );
   for (int sum, i=0; i < 4; i++) {
      sum = 0;
      for (int j=0; j < 3; j++)
         sum += cards_and_components[j][i];
      // If any of the 4 sums is not evenly divisible by 3, then the 3 cards do not form a set
      if (sum % 3 != 0)
         return false;
   }
   return true;
}

Here is an implementation ...

int number_of_sets = 0;
for (int i=0;   i < cards_showing.length - 2; i++)
  for (int j=i+1; j < cards_showing.length - 1; j++)
    for (int k=j+1; k < cards_showing.length;     k++) {
      test_set[0] = cards_showing[i];
      test_set[1] = cards_showing[j];
      test_set[2] = cards_showing[k];
      if (is_a_set( test_set )) {
        number_of_sets++;
        answer.append(test_set[0]+1).append(' ');
        answer.append(test_set[1]+1).append(' ');
        answer.append(test_set[2]+1).append("   ");
    } }
return number_of_sets;