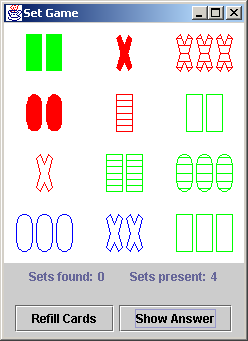
Set Game
The game is played by finding sets of three cards that are all the
same, or all different, across four independent "facets" or
"dimensions". These dimensions are: number, shape, color, and fill.
Each of these dimensions has three possible values. Number may be: one,
two, or three; color may be: red, green, or blue; shape may be: rectangle, X,
or O; and fill may be: open, striped, or solid.
|
Example sets:
|
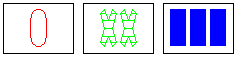 |
a SET
same: [none]
different: number, color, shape, fill
|
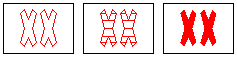 |
a SET
same: number, color, shape
different: fill
|
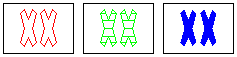 |
a SET
same: number, shape
different: color, fill
|
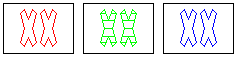 |
NOT a set
same: number, shape
different: color
wrong: fill |
|
To make it a set, one of the open fills needs to
be solid, or the striped fill needs to be open.
|
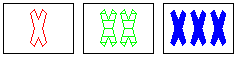 |
a SET
same: shape
different: color, number, fill
|
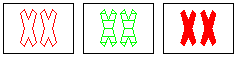 |
NOT a set
same: shape, number
different: fill
wrong: color |
|
To make it a set, one of the red colors needs to
be blue, or the green color needs to be red.
|
How many cards would you expect in a Set deck?
How would you uniquely identify each card?
Can you "compute" the value of each of the four
dimensions, or, does it need to be "stored"?
public static void compute_components( int card, int[] components ) {
components[0] = card % 3;
components[1] = card % 9 / 3;
components[2] = card % 27 / 9;
components[3] = card / 27;
}
What kind of algorithm will give us a decision on whether
3 cards constitute a set?
card1 0 0 1 1 2 2 0 0 1 2
card2 0 1 1 2 2 0 1 0 1 2
card3 1 1 2 2 0 0 2 0 1 2
set? no no no no no no yes yes yes yes
Above are all combinations of three 3-valued variables.
Is a pattern or source of leverage evident?
Here is an implementation ...
boolean is_a_set( int[] selected_cards ) {
int[][] cards_and_components = new int[3][4];
for (int i=0; i < 3; i++)
compute_components( selected_cards[i], cards_and_components[i] );
for (int sum, i=0; i < 4; i++) {
sum = 0;
for (int j=0; j < 3; j++)
sum += cards_and_components[j][i];
// If any of the 4 sums is not evenly divisible by 3, then the 3 cards do not form a set
if (sum % 3 != 0)
return false;
}
return true;
}
What kind of algorithm is necessary and sufficient to
compute all the sets present in an array of 12 cards?
What is the equation for "all combinations of X things
taken Y at a time"?
Here is an implementation ...
int number_of_sets = 0;
for (int i=0; i < cards_showing.length - 2; i++)
for (int j=i+1; j < cards_showing.length - 1; j++)
for (int k=j+1; k < cards_showing.length; k++) {
test_set[0] = cards_showing[i];
test_set[1] = cards_showing[j];
test_set[2] = cards_showing[k];
if (is_a_set( test_set )) {
number_of_sets++;
answer.append(test_set[0]+1).append(' ');
answer.append(test_set[1]+1).append(' ');
answer.append(test_set[2]+1).append(" ");
} }
return number_of_sets;
How about supplying the "view" component (Java GUI code)
and having the student design the "model" component (game engine)?
// incremental examples of loops, and growing to an algorithm for
// "all combinations of 12 things taken 3 at a time"
#include <iostream>
#include <string>
#include <sstream>
using std::cout;
using std::string;
using std::stringstream;
#if 0
// "for" loop, "+=" operator, one-line block of code doesn't need "{ }"
int main( void ) {
for (int number = 1; number < 11; number += 1)
cout << number << ' ';
cout << '\n';
}
// 1 2 3 4 5 6 7 8 9 10
// one loop inside another loop, accessing arrays
int main( void ) {
int nums[] = { 1,2,3,4,5 };
char chars[] = { 'a','b','c','d','e' };
for (int i=0; i < 5; ++i) {
for (int j=0; j < 5; ++j)
cout << nums[i] << chars[j] << ' ';
cout << '\n';
} }
// 1a 1b 1c 1d 1e
// 2a 2b 2c 2d 2e
// 3a 3b 3c 3d 3e
// 4a 4b 4c 4d 4e
// 5a 5b 5c 5d 5e
// defining and loading a 2-D array, using "integer division" that produces 0
int main( void ) {
int matrix[4][4];
for (int i=1; i <= 4; ++i)
for (int j=1; j <= 4; ++j)
// if i < j then 0, if j < i then 0, if i == j then 1
matrix[i-1][j-1] = (i/j) * (j/i);
for (int i=0; i < 4; ++i) {
for (int j=0; j < 4; ++j)
cout << matrix[i][j] << ' ';
cout << '\n';
} }
// 1 0 0 0
// 0 1 0 0
// 0 0 1 0
// 0 0 0 1
// each inner loop is "sized" by its outer loop
int main() {
cout << "all combinations of 5 things taken 3 at a time\n";
for (int i=0; i < 5 - 2; i++)
for (int j=i+1; j < 5 - 1; j++)
for (int k=j+1; k < 5; k++)
cout << i << j << k << " ";
cout << '\n';
}
// all combinations of 5 things taken 3 at a time ... 5 * 4 * 3 / 3 * 2 * 1
// 012 013 014 023 024 034 123 124 134 234
// all combinations of 12 things taken 3 at a time ... 12 * 11 * 10 / 3 * 2 * 1
int main( void ) { // equals 220
int count = 0, lines = 0;
char cards[] = { '1','2','3','4','5','6','7','8','9','a','b','c' };
for (int i=0; i < 12 - 2; ++i)
for (int j=i+1; j < 12 - 1; ++j) {
for (int k=j+1; k < 12; ++k) {
cout << cards[i] << cards[j] << cards[k] << ' ';
count += 1;
}
cout << '\n';
lines += 1;
}
cout << "count is " << count << ", lines is " << lines << '\n';
}
// 123 124 125 126 127 128 129 12a 12b 12c
// 134 135 136 137 138 139 13a 13b 13c
// 145 146 147 148 149 14a 14b 14c
// 156 157 158 159 15a 15b 15c
// 167 168 169 16a 16b 16c
// 178 179 17a 17b 17c
// 189 18a 18b 18c
// 19a 19b 19c
// 1ab 1ac
// 1bc
// 234 235 236 237 238 239 23a 23b 23c
// 245 246 247 248 249 24a 24b 24c
// ...
// 89a 89b 89c
// 8ab 8ac
// 8bc
// 9ab 9ac
// 9bc
// abc
// count is 220, lines is 55
#endif
// all permutations of the combinations of 5 things taken 3 at a time
void permute(string& str, int l, int r);
void swap( char& one, char& two );
int count = 0;
int main( void ) {
cout << "all permutations of 5 things taken 3 at a time\n";
cout << " (a permutation is an ordered combination)\n";
for (int i=0; i < 5 - 2; i++)
for (int j=i+1; j < 5 - 1; j++)
for (int k=j+1; k < 5; k++) {
stringstream ss;
ss << i << j << k;
string str = ss.str();
permute( str, 0, str.size() - 1 );
cout << '\n';
}
cout << "count is " << count << '\n';
}
// all permutations of 5 things taken 3 at a time ... 5 * 4 * 3
// (a permutation is an ordered combination)
// 012 021 102 120 210 201
// 013 031 103 130 310 301
// 014 041 104 140 410 401
// 023 032 203 230 320 302
// 024 042 204 240 420 402
// 034 043 304 340 430 403
// 123 132 213 231 321 312
// 124 142 214 241 421 412
// 134 143 314 341 431 413
// 234 243 324 342 432 423
// count is 60
// https://www.geeksforgeeks.org/write-a-c-program-to-print-all-permutations-of-a-given-string/
void permute(string& str, int l, int r) {
if (l == r) {
cout << str << ' ';
count += 1;
} else
for (int i = l; i <= r; i++) {
swap( str[l], str[i] );
//cout << 'p' << l << i << ' ';
permute( str, l + 1, r );
// backtrack
//cout << "b ";
swap( str[l], str[i] );
}
}
void swap( char& one, char& two ) {
char temp; temp = one; one = two; two = temp;
}
// A loop can often be used in place of many "if/else" statements.
// Many "if" statements in the 1960s language PL/I
DATES: PROC OPTIONS (MAIN);
READ: GET DATA (IYEAR, IDATE);
IF IDATE < 1 | IDATE > 366 | IYEAR < 0 THEN
RETURN;
IF IDATE <= 31 THEN GO TO JAN;
L = 1;
I = IYEAR/400;
IF I = IYEAR/400 THEN GO TO LEAP;
I = IYEAR/100;
IF I = IYEAR/100 THEN GO TO NOLEAP;
I = IYEAR/4;
IF I = IYEAR/4 THEN GO TO LEAP;
NOLEAP: L=0;
IF IDATE > 365 THEN RETURN;
LEAP: IF IDATE > 181 + L THEN GO TO G181;
IF IDATE > 90 + L THEN GO TO G90;
IF IDATE > 59 + L THEN GO TO G59;
MONTH = 2; IDAY = IDATE - 31; GO TO OUT;
G59: MONTH = 3; IDAY = IDATE - (59 + L); GO TO OUT;
G90: IF IDATE > 120 + L THEN GO TO G120;
MONTH = 4; IDAY = IDATE - (90 + L); GO TO OUT;
G120: IF IDATE > 151 + L THEN GO TO G151;
MONTH = 5; IDAY = IDATE - (120 + L); GO TO OUT;
G151: MONTH = 6; IDAY = IDATE - (151 + L); GO TO OUT;
G181: IF IDATE > 273 + L THEN GO TO G273;
IF IDATE > 243 + L THEN GO TO G243;
IF IDATE > 212 + L THEN GO TO G212;
MONTH = 7; IDAY = IDATE - (181 + L); GO TO OUT;
G212: MONTH = 8; IDAY = IDATE - (212 + L); GO TO OUT;
G243: MONTH = 9; IDAY = IDATE - (243 + L); GO TO OUT;
G273: IF IDATE > 334 + L THEN GO TO G334;
IF IDATE > 304 + L THEN GO TO G304;
MONTH = 10; IDAY = IDATE - (273 + L); GO TO OUT;
G304: MONTH = 11; IDAY = IDATE - (304 + L); GO TO OUT;
G334: MONTH = 12; IDAY = IDATE - (334 + L); GO TO OUT;
OUT: PUT DATA (MONTH,IDAY,IYEAR) SKIP;
GO TO READ;
JAN: MONTH=1; IDAY=IDATE; GOTO OUT;
END DATES;
// Many "if" stmts replaced with: days_per_month_table data structure, and a loop
String convert_julian( int year, int julian ) {
int[][] days_per_month_table = { {0,31,28,31,30,31,30,31,31,30,31,30,31},
{0,31,29,31,30,31,30,31,31,30,31,30,31} };
int leap = (year % 400 == 0 || year % 4 == 0 && year % 100 != 0) ? 1 : 0;
int i;
for (i=1; julian > days_per_month_table[leap][i]; i++)
julian -= days_per_month_table[leap][i];
int yr = year - (year/100 * 100);
return fill(i) + '/' + fill(julian) + '/' + fill(yr);
}
System.out.println( convert_julian( 1900, 60 ) ); // 03/01/00
System.out.println( convert_julian( 2000, 60 ) ); // 02/29/00
System.out.println( convert_julian( 2002, 60 ) ); // 03/01/02
System.out.println( convert_julian( 2004, 60 ) ); // 02/29/04
System.out.println( convert_julian( 1900, 365 ) ); // 12/31/00
System.out.println( convert_julian( 2000, 365 ) ); // 12/30/00
System.out.println( convert_julian( 2002, 365 ) ); // 12/31/02
System.out.println( convert_julian( 2004, 365 ) ); // 12/30/04
// the card game called Set: how to decide if 3 cards are a set
// 2 implementations: 4 levels of "if" statements, or, a loop and ingenuity
struct Card { int dimensions[4]; }; // 0-shape, 1-number, 2-color, 3-fill
// An implementation using 4 levels of "if" statements
#include
using std::set;
bool is_a_set( Card one, Card two, Card three ) {
// the set data structure only stores unique values
// (if values 1,1,2 are inserted, then values 1,2 are remembered)
set accumulate[4];
accumulate[0].insert( one.dimensions[0] );
accumulate[0].insert( two.dimensions[0] );
accumulate[0].insert( three.dimensions[0] );
accumulate[1].insert( one.dimensions[1] );
accumulate[1].insert( two.dimensions[1] );
accumulate[1].insert( three.dimensions[1] );
accumulate[2].insert( one.dimensions[2] );
accumulate[2].insert( two.dimensions[2] );
accumulate[2].insert( three.dimensions[2] );
accumulate[3].insert( one.dimensions[3] );
accumulate[3].insert( two.dimensions[3] );
accumulate[3].insert( three.dimensions[3] );
// success is: each of the 4 dimensions across all 3 cards must be:
// all the same value, or all different values
if (accumulate[0].size() == 1 || accumulate[0].size() == 3)
if (accumulate[1].size() == 1 || accumulate[1].size() == 3)
if (accumulate[2].size() == 1 || accumulate[2].size() == 3)
if (accumulate[3].size() == 1 || accumulate[3].size() == 3)
return true;
return false;
}
// An implementation using a loop and an ingenious algorithm
// card1 0 0 1 1 2 2 0 0 1 2
// card2 0 1 1 2 2 0 1 0 1 2
// card3 1 1 2 2 0 0 2 0 1 2
// sum 1 2 4 5 4 2 3 0 3 6
// % 3 1 2 1 2 1 2 0 0 0 0
// set? no no no no no no yes yes yes yes
// algorithm: use the modulus operator to "compute" the desired decision
bool is_a_set( Card one, Card two, Card three ) {
// This loop replaces the 4 "if" statements in the previous implementation
for (int i=0; i < 4; ++i)
// this "algorithm" demonstrates insight and leverage
// if any dimension fails the set criteria, then return false immediately
if ((one.dimensions[i] + two.dimensions[i] + three.dimensions[i]) % 3 != 0)
return false;
// only return true if all 4 dimensions satisfy the criteria to be a set
return true;
}
// Generate and evaluate all combinations of 12 cards taken 3 at a time
int compute_sets_present( Card cards_showing[], string& answer_str ) {
int number_of_sets = 0;
stringstream answer;
for (int i=0; i < 12 - 2; i++)
for (int j=i+1; j < 12 - 1; j++)
for (int k=j+1; k < 12; k++)
if (is_a_set( cards_showing[i],cards_showing[j],cards_showing[k] )) {
number_of_sets++;
answer << (i+1) << ' ';
answer << (j+1) << ' ';
answer << (k+1) << " ";
}
answer_str = answer.str();
return number_of_sets;
}
void initialize_card( int index, Card& card ) {
// use modulus operator and integer division to compute the card's 4 dimensions
card.dimensions[0] = index % 3;
card.dimensions[1] = index % 9 / 3;
card.dimensions[2] = index % 27 / 9;
card.dimensions[3] = index / 27;
}
int main( void ) {
Card cards[81];
for (int i=0; i < 81; ++i)
initialize_card( i, cards[i] );
string answer_str;
int num_sets = compute_sets_present( cards, answer_str );
cout << "number of sets is " << num_sets << '\n';
cout << answer_str << '\n';
}
// number of sets is 13
// 1 2 3 1 4 7 1 5 9 1 6 8 2 4 9 2 5 8 2 6 7
// 3 4 8 3 5 7 3 6 9 4 5 6 7 8 9 10 11 12






