I believe sophistication, or elegance, or craftsmanship are subjects better caught than taught. They can be discussed, and admired, and sought after; but they cannot be neatly packaged or prescribed by a methodology or checklist. This article is an attempt to document a personal pilgrimage of epiphany in such a way that some amount of insight might be covertly "caught". Perhaps the following discussion is best viewed as a parable - a simple story that indirectly illustrates a not-so-simple principle.
I will discuss a design for the game Mastermind that balances object-oriented design, and more general data structure and algorithm design. The "gang of four" State design pattern and several interesting algorithms will be demonstrated. The first several iterations will implement a solitaire version of the game where the user solves the puzzle. The latter segments will implement a state machine that solves any puzzle supplied by the user.
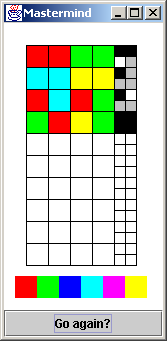 In the original Mastermind board game, one player picks four colored pegs (from
a palette of six colors) and places them in some random order behind a
barrier. A single color may be chosen more than once. [The example to the
right has a solution of: green, red, yellow, green.] The other player now
tries to solve the puzzle by making guesses with four colored pegs at a time.
The original player "scores" each guess by providing black pegs for elements of
a guess that are 100% correct (correct color in the correct position), and
white pegs for elements that are 50% correct (correct color in the wrong
position). Below is an example of a game using the letters 'a' through 'f',
instead of six colors.
In the original Mastermind board game, one player picks four colored pegs (from
a palette of six colors) and places them in some random order behind a
barrier. A single color may be chosen more than once. [The example to the
right has a solution of: green, red, yellow, green.] The other player now
tries to solve the puzzle by making guesses with four colored pegs at a time.
The original player "scores" each guess by providing black pegs for elements of
a guess that are 100% correct (correct color in the correct position), and
white pegs for elements that are 50% correct (correct color in the wrong
position). Below is an example of a game using the letters 'a' through 'f',
instead of six colors.
Enter guess: bbcc
1 0
Enter guess: ddee
2 0
Enter guess: bdef
2 0
Enter guess: ddcf
0 0
Enter guess: baee
4 0
The first player chose four random letters that are not visible. The second
player guessed the sequence "bbcc". The score returned was: one letter is 100%
correct, and no letters are 50% correct. The second guess was "ddee", and the
score was two that are entirely correct and 0 that are partially correct. We
now know that out of the letters b, c, d, and e, we have 3 of the 4 letters
identified. So the one remaining letter is either a or f.Taking a wild stab on the third guess, the second player unilaterally decides the first b in the first guess is correct, the second d and first e of the second guess are correct, and f is the remaining character. The score returned is not very exciting. As more guesses are made, the process of elimination makes it possible to focus in on the answer. Each new guess must be consistent with the feedback received on all previous guesses. If the new guess cannot reproduce the score of all previous guesses, then it cannot be the answer.
The fourth guess could produce the score assigned to each of the three previous guesses, so it is registered. The score returned might initially be viewed as entirely negative - but in reality, the exact opposite is true. We now know there are no d's, c's, or f's in the answer. There can only be one b (from the first guess), two e's from the second guess, and one a in the second position (from the third guess). A score of 4 "black pegs" and 0 "white pegs" indicates the puzzle has been solved.
The previous example was peculiar in not returning any "white pegs". Let's try another. So as not to introduce more "unknowns" than our carbon-based equation processor can handle, the first two guesses are limited to two characters only.
Enter guess: ccdd
1 0
Enter guess: eeff
0 3
Enter guess: cfee
4 0
The strategy of picking characters that do not overlap in the first two
guesses has paid off handsomely in this case. If the total of the black and
white answers equals four, then we know the two remaining characters are not
part of the puzzle. The second score is telling us there are at least 2 e's
or 2 f's, and they are not in the positions portrayed in the guess. The
only logic behind the third guess is that it does not disagree with the
feedback on the first two guesses - there is no substitute for dumb luck.
Here is a main() that will give us the sessions shown above.
public static void main( String[] args ) throws IOException {
BufferedReader rdr = new BufferedReader( new InputStreamReader( System.in ));
String str = null;
Board board = new Board();
int[] response = new int[2];
while (response[0] != Board.NUM_SLOTS) {
System.out.print( "Enter guess: " );
str = rdr.readLine();
board.evaluate( str.toCharArray(), response );
System.out.println( " " + response[0] + ' ' + response[1] );
} }
public class Board {
public static final int NUM_CHOICES = 6;
public static final int NUM_SLOTS = 4;
Next, we could model a position (or slot) in a puzzle as an object of
type "Slot". Each object will assign itself a random character when it
is created, and an array of these objects will represent the puzzle.
public class Board {
private Slot[] answer = new Slot[NUM_SLOTS];
private class Slot {
private char value;
public Slot() {
value = (char) ('a' + (int) (Math.random()*1000) % NUM_CHOICES);
} }
public Board() {
for (int i=0; i < NUM_SLOTS; i++)
answer[i] = new Slot();
}
When an evaluate() request comes in, computing the "black" answer
(correct letters in the correct positions) is straight-forward,
simply count the number of elements in the "guess" array that correspond
to elements in the "answer" array.
public void evaluate( char[] guess, int[] response ) {
response[0] = 0;
for (int i=0; i < answer.length; i++)
if (answer[i].equalsChar( guess[i] ))
response[0]++;
The tricky part is computing the "white" answer (correct letters in the wrong
positions). All the Slot objects and
guess characters that contributed to the "black" answer must not participate
in the computation of the white response. A "collection" capability that can test
for membership and easily remove an element would be very useful. The
standard library's LinkedList class will work nicely. The evaluate() function
shown above will need to be amended to populate a LinkedList for both the
answer array and the guess array, and then remove elements as black matches
are found.
public void evaluate( char[] guess, int[] response ) {
response[0] = response[1] = 0;
LinkedList guessLL = new LinkedList();
LinkedList answerLL = new LinkedList();
for (int i=0; i < NUM_SLOTS; i++) {
guessLL.add( new Character( guess[i] ));
answerLL.add( answer[i] );
}
ListIterator aIt = answerLL.listIterator(0);
ListIterator gIt = guessLL.listIterator(0);
while (aIt.hasNext())
if (((Slot)aIt.next()).equals( (Character) gIt.next() )) {
response[0]++;
aIt.remove();
gIt.remove();
}
The final piece of evaluate() is to step through each element in the
guess linked list and check for membership in the answer linked list. When
a match is found, the element in the answer linked list is removed so that
it does not get paired up with in other guess characters.
gIt = guessLL.listIterator(0);
Object obj;
while (gIt.hasNext())
if (answerLL.contains( obj = new Slot( (Character) gIt.next() ))) {
response[1]++;
answerLL.remove( obj );
}
That's it for the first approach. Let's step back and take an accounting
of the overhead. There are the Slot objects, the 2 LinkedList objects and
their ListIterator objects, the
Character objects (because Java collection classes do not accept primitive
data types), and the extra Slot objects created to get the contains()
and remove() methods to work.[The complete application can be found here.]
There ought to be an easier way to do this.
private char[] answer = new char[NUM_SLOTS];
private boolean[] answerUsed = new boolean[NUM_SLOTS];
private boolean[] guessUsed = new boolean[NUM_SLOTS];
public Board() {
// populate answer array with random characters
for (int i=0; i < NUM_SLOTS; i++)
answer[i] = (char) ('a' + (int) (Math.random()*1000) % NUM_CHOICES);
}
public void evaluate( char[] guess, int[] response ) {
response[0] = response[1] = 0;
// initialize boolean arrays
for (int i=0; i < NUM_SLOTS; i++)
guessUsed[i] = answerUsed[i] = false;
// compute black answer
for (int i=0; i < NUM_SLOTS; i++)
if (guess[i] == answer[i]) {
response[0]++;
guessUsed[i] = answerUsed[i] = true;
}
To compute the white answer, one loop variable is used to
control traversal through the guess array, and a second loop variable
is used to control traversal through the answer array. If a guess
character is matched in the answer array: some bookkeeping
is taken care of, the remainder of the inner loop is skipped, and the
next iteration of the outer loop proceeds.
// compute white answer
for (int i=0; i < NUM_SLOTS; i++)
if ( ! guessUsed[i])
for (int j=0; j < NUM_SLOTS; j++)
if ( ! answerUsed[j])
if (guess[i] == answer[j]) {
response[1]++;
guessUsed[i] = answerUsed[j] = true;
break;
}
[The complete application can be found here.]
Insight interlude. Fred Brooks has suggested, "Too often we confuse effort and progress." [ 1 ] Gerald Weinberg has observed, "We often judge how difficult a program is by how hard a programmer works on it. Using this sort of measure, we can easily fall into believing that the worst programmers are the best." [ 2 ]
Sometimes I wonder about all the "effort" (the process, the notation, the orthodoxy) that has grown up around the object-oriented design paradigm. While remarkably effective at handling complexity and change, it is not the sole source of inspiration and leverage. In this context, OO praxis might be characterized as the sledge hammer approach, when a tack hammer would be more appropriate.
Insight interlude. It is a common problem solving technique to translate a problem from one "domain" to another "domain", from one "space-time continuum" to a different "space-time continuum". For example, doing multiplication of vectors is difficult in a cartesian coordinate space, but it is simple in a polar coordinate space. Doing addition of vectors is difficult in polar coordinates, but it is trivial in cartesian coordinates.
This strategy of migrating our point of reference can pay big dividends in our Mastermind design. Our current implementation has focused on arrays of characters. But if we counted the number of occurrences of each possible letter, and changed our focus to arrays of integers, we can make computing the white answer easy. Let's say the answer is "abfb" and the guess is "eaba". The corresponding "count" arrays would be -
character integer
array count array
a b c d e f
answer abfb 1 2 0 0 0 1
guess ebaa 2 1 0 0 1 0
Here is code for initializing the data structures.
private char[] answer = new char[NUM_SLOTS];
private int[] answerChars = new int[NUM_CHOICES];
private int[] guessChars = new int[NUM_CHOICES];
public Board() {
// populate answer array with random characters
for (int i=0; i < NUM_SLOTS; i++)
answer[i] = (char) ('a' + (int) (Math.random()*1000) % NUM_CHOICES);
// initialize the answer count array
for (int i=0; i < NUM_SLOTS; i++)
answerChars[ answer[i] - 'a' ]++;
public void evaluate( char[] guess, int[] response ) {
// initialize the guess count array
for (int i=0; i < NUM_CHOICES; i++)
guessChars[i] = 0;
for (int i=0; i < NUM_SLOTS; i++)
guessChars[ guess[i] - 'a' ]++;
Given this new perspective, we can compute the white answer by taking the
minimum of each answer count and guess count pair. In the example, the player
guessed two a's when there is only one in the answer. The "overlap" between
the answer and the guess (relative to the letter 'a') is one. With the letter
'b', the situation is reversed. The guess contains two b's when only one
exists in the answer. Again, the "overlap" is one. The general algorithm
for computing the white answer becomes: sum the minimum of corresponding
elements in the answer and guess count arrays.This algorithm does not take into account the black component of a score. But, since the black answer is a proper subset of our current white answer; all that needs to happen to amend our white answer is to subtract its black answer component.
// over-compute white answer
for (int i=0; i < NUM_CHOICES; i++)
response[1] += Math.min( guessChars[i], answerChars[i] );
// compute black answer
for (int i=0; i < NUM_SLOTS; i++)
if (guess[i] == answer[i]) response[0]++;
// eliminate the overlap
response[1] = response[1] - response[0];
}
[The complete application can be found here.]
The more general problem is often easier to solve, and in programming, the more general design may be easier to implement, may operate faster on the machine, and can actually be better understood by the user. In addition, it will almost certainly be easier to maintain, for often we won't have to change anything at all to meet changing circumstances that fall within its range of generality. [ 3 ]When I first read this, I was studying the topic of reuse. The assertion suggests that reuse is not the "one size fits all, 80% solution". Reuse can, and should, be the 110% solution. But that will be the case only if significant effort is invested in accruing insight, and not simply spent following a prescribed checklist.
Let's call the initial state of this state machine GuessOne. It picks two random letters for its guess. The second state (aka GuessTwo) uses two different random letters.
The third state (GuessCompute) makes fairly random guesses until the total of black plus white equals four (the number of slots in the board). These guesses are not entirely random though. Each must not contradict any feedback returned from previous guesses.
As soon as "black + white == 4", the final state is entered - GuessPermute. At this point, all the letters have been identified. What remains is to figure out the correct ordering of the known letters.
Several "rules" can be employed while processing a puzzle with this state machine. Rule one: if "black + white == 0", then each letter in the guess is not in the answer. This kind of feedback significantly limits the number of remaining possibilities. Here is a silicon-based player whose first guess demonstrates this rule.
Enter puzzle: acab
eeff 0 0
eliminating e
eliminating e
eliminating f
eliminating f
aabb 2 1
possible guesses eliminated were 18
caba 0 4
removing c from position 1
removing a from position 2
removing b from position 3
removing a from position 4
possible guesses eliminated were 3
acab 4 0
The user typed in the puzzle "acab". The Solver guessed "eeff". When
black + white came back zero, e and f were eliminated completely from
future deliberations.Rule two: if "black == 0" then each letter in the guess cannot be at its same position in the answer. This rule doesn't offer nearly as much leverage as rule one, but every little bit helps. The third guess above demonstrates rule two at work.
Rule three: if "black + white == 4", then set the state machine's "current state" to GuessPermute. The logic behind this was already discussed above. The example below goes straight from state GuessOne to state GuessPermute and stays there until the puzzle is solved.
Enter puzzle: fafa
ffaa 2 2
possible guesses eliminated were 1
afaf 0 4
possible guesses eliminated were 2
fafa 4 0
There is one additional special case rule: if black plus white from both
GuessOne and
GuessTwo equals 4, then the two letters not used in the two guesses cannot
be in the answer. This is true because the four letters chosen for the
first two guesses are guaranteed not to overlap. Here is an example.
Enter puzzle: afae
ddee 1 0
ffaa 2 1
eliminating b
eliminating c
possible guesses eliminated were 35
faea 0 4
removing f from position 1
removing a from position 2
removing e from position 3
removing a from position 4
possible guesses eliminated were 33
afae 4 0
Just as a person can visually inspect the responses from
previous guesses, and rule out invalid guesses; a program
can do the same. The output of the form "possible guesses
eliminated ..." is some status information that shows how much
work the Solver state machine has processed before issuing a
guess that does not contradict any feedback returned from
previous guesses.The code that drives the Solver application is shown below.
public static void main( String[] args ) throws IOException {
BufferedReader rdr = new BufferedReader( new InputStreamReader( System.in ));
String str = null;
System.out.print( "Enter puzzle: " );
str = rdr.readLine(); }
Board b = new Board( str.toCharArray() );
Solver s = new Solver( b );
s.solve();
} }
The "current state" abstraction is modeled as an interface, and each of the concrete states we have discussed so far extends that interface. The State derived classes are implemented as Singletons with a static inst() accessor function. The logic that moves the state machine from one state to the next is generally encapsulated in the State derived classes. Here is the code we have discussed so far.
public class Solver {
private Board b;
private State current;
public Solver( Board bored ) {
b = bored;
current = GuessOne.inst();
}
public void setCurrent( State s ) { current = s; }
public void solve() { while ( ! current.solve( this )); }
}
interface State { boolean solve( Solver wrapper ); }
class GuessOne implements State {
private static GuessOne me = new GuessOne();
public static GuessOne inst() { return me; }
public boolean solve( Solver wrapper ) {
public class Solver {
private Slot[] slots = new Slot[Board.NUM_SLOTS];
....
public class Slot {
private StringBuffer choices = new StringBuffer();
public Slot() {
for (int i=0; i < Board.NUM_CHOICES; i++)
choices.append( (char)('a'+i) );
}
public void remove( char ch ) {
int i;
for (i=0; i < choices.length(); i++)
if (choices.charAt(i) == ch) break;
if (i < choices.length()) choices.deleteCharAt( i );
} }
When GuessCompute becomes the current state, somebody needs to be able
to step through all possible permutations of all letters that are still
"in play".Insight interlude. How can we step through all combinations of several variables, each of which may have a different number of legal values?
Perhaps the model of an odometer is instructive. We could put the legal values for each variable on a cylinder, line the cylinders up side by side, and implement a "carry" capability that can increment the next cylinder when the current one has achieved a complete rotation. To enumerate all combinations would then be a matter of "counting" from the lowest combination to the highest.
This counting behavior can largely be the responsibility of the Slot class. The coordination that needs to exist between Slot objects will be implemented in the Solver class and discussed later. Here is the code for Slot's portion of the counting functionality. Because two values must be returned, a "struct" has been defined to accommodate Java's limited parameter passing capability.
class OutParameterStruct {
char next;
boolean carry;
}
public class Slot {
private int next;
public void getNext( OutParameterStruct s ) {
s.carry = false;
if (++next == choices.length()) {
next = 0;
s.carry = true;
}
s.next = choices.charAt(next);
}
The applyRules() method oversees the application of the three rules previously discussed. If rule three succeeds, the state machine is put in the GuessPermute state and true is returned. Otherwise, the GuessOne state needs to communicate to the GuessTwo state what letter it should guess next, and, the total of its black and white answers. GuessOne then sets the current state of the state machine to GuessTwo.
class GuessOne implements State {
public boolean solve( Solver wrapper ) {
char first = (char)('a' + ((int)(Math.random() * 29)) % Board.NUM_CHOICES);
char second = (char)('a' + (first+1-'a') % Board.NUM_CHOICES);
char[] guess = new char[Board.NUM_SLOTS];
int i;
for (i=0; i < Board.NUM_SLOTS / 2; i++) guess[i] = first;
for ( ; i < Board.NUM_SLOTS; i++) guess[i] = second;
int[] answer = new int[2];
if (wrapper.evaluate( guess, answer )) return true;
// If rule 3 sets the current state to GuessPermute, then don't set the
// current state to GuessTwo, but do return false to indicate that the
// puzzle has not yet been solved
if (wrapper.applyRules( guess, answer )) return false;
// Pass on to the next state: the next random letter, and the total of black
// plus white
GuessTwo.inst().setState(
(char)('a' + (second+1-'a') % Board.NUM_CHOICES), answer[0] + answer[1] );
wrapper.setCurrent( GuessTwo.inst() );
return false;
} }
public class Solver {
private Vector history = new Vector();
public boolean evaluate( char[] guess, int[] response ) {
b.evaluate( guess, response );
for (int i=0; i < guess.length; i++) System.out.print( guess[i] );
System.out.println( " " + response[0] + " " + response[1] );
history.add( new TurnStruct( guess, response ) );
return response[0] == Board.NUM_SLOTS;
}
The applyRules() method is fairly straight-forward. If rule one
succeeds, there is no need to apply rule two. If rule three succeeds:
the current guess array is registered with the GuessPermute singleton,
the state machine is vectored to the GuessPermute state, and default
flow of control is skipped.
public boolean applyRules( char[] guess, int[] response ) {
if ( ! ruleOne( guess, response )) ruleTwo( guess, response );
return ruleThree( guess, response );
}
public boolean ruleOne( char[] guess, int[] response ) {
if (response[0] + response[1] == 0) {
for (int i=0; i < guess.length; i++)
eliminate( guess[i] );
return true;
} else return false;
}
public boolean ruleTwo( char[] guess, int[] response ) {
if (response[0] == 0) {
for (int i=0; i < guess.length; i++) {
System.out.println( " removing " + guess[i]
+ " from position " + (i+1) );
slots[i].remove( guess[i] );
}
return true;
} else return false;
}
public boolean ruleThree( char[] guess, int[] response ) {
if (response[0] + response[1] == Board.NUM_SLOTS) {
GuessPermute.inst().setState( guess );
current = GuessPermute.inst();
return true;
} else return false;
}
class GuessTwo implements State {
private char first;
private int firstTotal;
public void setState( char n, int total ) {
first = n;
firstTotal = total;
}
public boolean solve( Solver wrapper ) {
char second = (char)('a' + (first+1-'a') % Board.NUM_CHOICES);
char[] guess = new char[Board.NUM_SLOTS];
int i;
for (i=0; i < Board.NUM_SLOTS / 2; i++) guess[i] = first;
for ( ; i < Board.NUM_SLOTS; i++) guess[i] = second;
int[] answer = new int[2];
if (wrapper.evaluate( guess, answer )) return true;
if (wrapper.applyRules( guess, answer )) return false;
if (firstTotal + answer[0] + answer[1] == Board.NUM_SLOTS) {
for (int j=0; j < Board.NUM_CHOICES - 4; j++)
wrapper.eliminate( (char)('a' + (second+1+j-'a') % Board.NUM_CHOICES) );
}
wrapper.setCurrent( GuessCompute.inst() );
return false;
} }
class GuessCompute implements State {
public boolean solve( Solver wrapper ) {
char[] a;
int[] answer = new int[2];
a = wrapper.first_count_string();
while (true) {
if (a == null) return true;
if (wrapper.isConsistent( a )) {
wrapper.reportNotConsistent();
if (wrapper.evaluate( a, answer )) return true;
if (wrapper.ruleOne( a, answer ) || wrapper.ruleTwo( a, answer )) {
a = wrapper.first_count_string();
continue;
}
if (wrapper.ruleThree( a, answer )) return false;
}
a = wrapper.next_count_string();
} } }
Earlier, the "history list" of previous guesses was introduced.
That list is used by Solver's isConsistent() method. It
is a simple vector of structs. Before each guess is made,
it is checked against all previous responses returned to ensure
that the guess is really worth making.Insight interlude. What does it mean for a guess to be "consistent"? The entire goal of the game is to identify the answer. Each guess that is made should potentially be the answer. A guess cannot possibly be the answer if it could not be used to produce the responses returned from all previous guesses.
This means the Solver class needs an evaluate() method that mirrors the functionality already available in the Board class. Instead of duplicating that code, it would make more sense to: add a new method to Board that accepts 4 array arguments, move the body of the current evaluate() to the new method, and call the new 4-argument evaluate() from the original 2-argument evaluate().
class TurnStruct {
public char[] guess;
public int black, white;
public TurnStruct( char[] g, int[] ans ) {
guess = new char[Board.NUM_SLOTS];
for (int i=0; i < Board.NUM_SLOTS; i++) guess[i] = g[i];
black = ans[0]; white = ans[1];
} }
public class Solver {
private int[] answerChars = new int[Board.NUM_CHOICES];
private int notConsistent = 0;
public boolean isConsistent( char[] a ) {
for (int j=0; j < Board.NUM_CHOICES; j++) answerChars[j] = 0;
for (int j=0; j < Board.NUM_SLOTS; j++) answerChars[ a[j] - 'a' ]++;
for (int i=0; i < history.size(); i++) {
TurnStruct t = (TurnStruct) history.elementAt(i);
b.evaluate( a, answerChars, t.guess, response );
if (response[0] != t.black || response[1] != t.white) {
notConsistent++;
return false;
} }
return true;
}
....
public class Board {
private char[] answerAttr = new char[NUM_SLOTS];
private int[] answerCharsAttr = new int[NUM_CHOICES];
public void evaluate( char[] guess, int[] response ) {
evaluate( answerAttr, answerCharsAttr, guess, response );
}
public void evaluate( char[] answer, int[] answerChars,
char[] guess, int[] response ) {
....
The Slot objects were discussed in their own section above. They
are fairly sentient, but they are not smart enough to enumerate all
the "count" strings required by the GuessCompute state. The Solver
object takes the odometer-like output from each Slot object, and
composes an exhaustive list of count strings.
public class Slot {
private StringBuffer choices = new StringBuffer();
private int next;
public char reset() {
next = 0;
return choices.charAt( next );
}
public void getNext( OutParameterStruct s ) {
s.carry = false;
if (++next == choices.length()) { next = 0; s.carry = true; }
s.next = choices.charAt(next);
}
....
public class Solver {
private char[] next = new char[Board.NUM_SLOTS];
private OutParameterStruct s = new OutParameterStruct();
public char[] first_count_string() {
for (int i=0; i < Board.NUM_SLOTS; i++) next[i] = slots[i].reset();
return next;
}
public char[] next_count_string() {
int x = 0;
slots[x].getNext( s );
next[x] = s.next;
while (s.carry) {
slots[++x].getNext( s );
next[x] = s.next;
if (x == Board.NUM_SLOTS-1 && s.carry) return null;
}
return next;
}
Insight interlude. Knowing the answer to every possible problem is not a realistic goal. Knowing where to find the answer is considerably more practical. The best way to develop an algorithm is to not develop it; instead, reuse an existing algorithm. In this case, there is an algorithm in the standard library of C++ that is just what is needed. It is called next_permutation(). The implementation summarized below came from SGI's STL Web page. [ 4 ]
class GuessPermute implements State {
private int[] answer = new int[2];
private char[] a;
public void setState( char[] ans ) { a = ans; }
public boolean solve( Solver wrapper ) {
sort();
while (true) {
if (wrapper.isConsistent( a )) {
wrapper.reportNotConsistent();
if (wrapper.evaluate( a, answer )) return true;
}
next_permutation_string();
} }
private boolean next_permutation_string() {
char t;
if (a.length < 2) return false;
for (int i=a.length-1, ii, j; ; ) {
ii = i--;
if (a[i] < a[ii]) {
j = a.length;
while ( ! (a[i] < a[--j])) { }
t=a[i]; a[i] = a[j]; a[j] = t; // swap
reverse( ii, a.length-1 );
return true;
}
if (i == 0) {
reverse( 0, a.length-1 );
return false;
} } }
Rather than trying to explain the next_permutation_string()
algorithm, permit me to just list four data sets it produces. You
will notice "swap" and "reverse" qualities in its output.
aabb abab abba baab baba bbaa
abc acb bac bca cab cba
abcd abdc acbd acdb adbc adcb bacd badc bcad bcda bdac bdca
cabd cadb cbad cbda cdab cdba dabc dacb dbac dbca dcab dcba
abcde abced abdce abdec abecd abedc acbde acbed acdbe acdeb acebd acedb
adbce adbec adcbe adceb adebc adecb aebcd aebdc aecbd aecdb aedbc aedcb
bacde baced badce badec baecd baedc bcade bcaed bcdae bcdea bcead bceda
bdace bdaec bdcae bdcea bdeac bdeca beacd beadc becad becda bedac bedca
cabde cabed cadbe cadeb caebd caedb cbade cbaed cbdae cbdea cbead cbeda
cdabe cdaeb cdbae cdbea cdeab cdeba ceabd ceadb cebad cebda cedab cedba
dabce dabec dacbe daceb daebc daecb dbace dbaec dbcae dbcea dbeac dbeca
dcabe dcaeb dcbae dcbea dceab dceba deabc deacb debac debca decab decba
eabcd eabdc eacbd eacdb eadbc eadcb ebacd ebadc ebcad ebcda ebdac ebdca
ecabd ecadb ecbad ecbda ecdab ecdba edabc edacb edbac edbca edcab edcba
Enter puzzle: fcaf
ffaa 2 1
bbcc 0 1
removing b from position 1
removing b from position 2
removing c from position 3
removing c from position 4
eliminating d
eliminating e
possible guesses eliminated were 11
faba 1 1
possible guesses eliminated were 13
cffa 0 4
removing c from position 1
removing f from position 2
removing f from position 3
removing a from position 4
possible guesses eliminated were 11
fcaf 4 0
State GuessOne offers up the guess "ffaa" and changes the current state to
GuessTwo. That state guesses "bbcc". Since "black == 0", none of the
characters in the guess can possibly be at their current position, so each
is "removed". Additionally, since the total feedback from guesses one and
two equals 4, then characters d and e cannot be in the answer, and they
are "eliminated".State GuessTwo changes the current state to GuessCompute. That state starts computing "count" strings, testing each one against all prior guesses. Eleven possible strings are eliminated before "faba" is computed. This string agrees with the guess and response of both previous guesses. The f and second a could account for the 2 black, and the first a could account for the 1 white of the first guess. The b could account for the 1 white of the second guess.
State GuessCompute then discards thirteen more strings before "cffa" is computed. Please justify for yourself that an answer of "cffa" would in fact produce the response from each of the previous three guesses. Because "black == 0", each character is removed from its current position. At this point, "black + white == 4", so GuessCompute changes the current state to GuessPermute.
State GuessPermute discards eleven possible permutations before finding its first consistent candidate, and that guess is exactly what the user specified at the outset.
[The complete application can be found here.]